Applications of Propositional Logic

Logic has many important applications to mathematics, computer science, and other disciplines:

• In the specification of software and hardware.
  Nonsense claim made in book:
  "because these specifications need to be precise before development begins."
  It is rare in software development that this could possibly be the case.
• To design computer circuits.
• To construct computer programs.
• To verify the correctness of programs.
• To build expert systems.
• To analyze and solve many familiar puzzles.

Example:
"You will pass this course only if you read the material and do the problems."
p = "You will pass this course."
r = "Read the material."
d = "Do the problems."
Translation: p ⇔ r ∧ d

Our textbook makes the following claim:

Translating sentences in natural language (such as English) into logical expressions is an essential part of specifying both hardware and software systems. System and software engineers take requirements in natural language and produce precise and unambiguous specifications that can be used as the basis for system development.

This claim is simply not true when it comes to software development: very little real-world development takes place by trying to first formally specify all requirements; when that is attempted, it rarely works.

Searches of things like the web, or large databses, such as our library's catalog, often can be done using logical operators.
Example: Mexico AND university -New
Searches Google for pages containing "Mexico" and "university" but not "New".

• The Muddy Children Puzzle
• Knights and Knaves

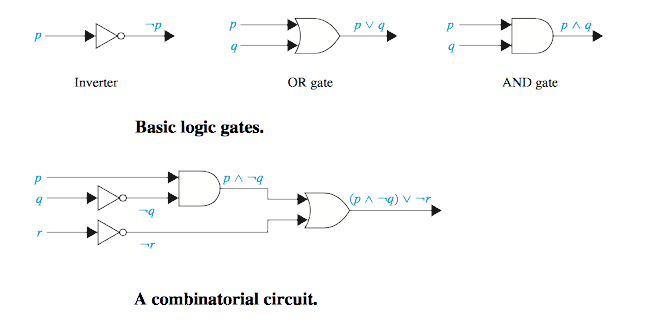
Propositional logic can be applied to the design of computer hardware. A logic circuit (or digital circuit) receives input signals p₁, p₂, . . . , p_n, each a bit [either 0 (off) or 1 (on)], and produces output signals s₁, s₂, . . . , s_n, each a bit. In this section we only treat logic circuits with a single output signal.

1. Formal logic can be used:
1. all answers are correct
2. to design computer circuits
3. to construct computer programs
4. to analyze puzzles
2. The correct translation of the sentence "If it rains it pours" (where r = "it rains" and p = "it pours") is:
1. p ∨ r
2. p ⇒ r
3. r ⇒ p
4. r ∧ p
3. An OR gate:
1. takes two inputs and sends out a positive signal if one or the other sends it a positive signal.
2. takes two inputs and sends out a positive signal if both sent it a positive signal
3. takes two inputs and sends out a positive signal if neither sent it a positive signal
4. Which of the following is not a connective?
1. NOT
2. ON
3. NOR
4. AND
5. What's the inverse of "If today is a Sunday, then it is sunny"?
1. If today is a Sunday, then it is not sunny
2. If it is sunny, then today is a Sunday
3. If today is not a Sunday, then it is not sunny
4. If it is not sunny, then today is not a Sunday