
A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a ∈ A to denote that a is an element of the set A. The notation a ∉ A denotes that a is not an element of the set A. A set is an unordered collection of objects, called elements or members of the set. A set is said to contain its elements. We write a ∈ A to denote that a is an element of the set A. The notation a ∉ A denotes that a is not an element of the set A.
There are two ways of describing,
or specifying the members of, a set
The two ways are:
Roster method:
refers to a technique in representing a set
by directly listing all of its elements,
which are separated by commas and enclosed
by a pair of curly brackets.
Example: The set V of all vowels
in the English alphabet can be
written as V = {a, e, i, o, u}.
Example: The set V of all vowels
in the English alphabet can be
written as V = {a, e, i, o, u}.
Set builder:
We characterize all
those elements in the set by stating the
property or properties they must have to be members.
For instance, the set O of all odd
positive integers less than 10 can be written as
O = {x | x is an odd positive integer less than 10}
or, specifying the universe as the set of positive
property or properties they
must have to be members.
For instance, the set O of all odd
positive integers less than 10 can be written as
O = {x | x is an odd
positive integer less than 10}
or, specifying the universe as the set of positive
integers, as
O={x ∈ ℤ+ |
x is odd and x < 10}.
We often use this type of notation to describe sets
when it is impossible to list all the elements
of the set. For instance, the set Q+ of all
of the set. For instance, the set ℚ+ of all
positive rational numbers can be written as
ℚ+={x ∈ ℝ
| x = p / q,
for some positive integers p and q}.
These sets, each denoted using a boldface letter,
play an important role in discrete mathematics:
ℕ
= {0, 1, 2, 3, ...}, the set of natural numbers
ℤ =
{..., -2, -1, 0, 1, 2, ...}, the set of integers
ℤ+
= {1, 2, 3, ...}, the set of positive integers
ℚ =
{p/q | p ∈ Z, q ∈ Z, and q ≠ 0},
the set of rational numbers
{p/q | p ∈ Z,
q ∈ Z, and q ≠ 0},
the set of rational numbers
ℝ, the set of real numbers
ℝ+, the set of positive real numbers
ℂ, the set of complex numbers.
The Empty Set:
The set with no members: ∅
Naive Set Theory:
Russell's Paradox

A Venn diagram (also called primary diagram, set diagram or logic diagram) is a diagram that shows all possible logical relations between a finite collection of different sets. These diagrams depict elements as points in the plane, and sets as regions inside closed curves.

The set A is a subset of B
iff every element of A is
also an element of B. We use the notation A ⊆ B
to indicate that A is a subset of the set
B.
We see that A ⊆ B if and only if the
quantification ∀x(x ∈ A → x ∈ B)
is true.

The set A is a subset of B
iff every element of A is
also an element of B.
We use the notation A ⊆ B
to indicate that A
is a subset of the set B.
We see that A ⊆ B
if and only if the quantification
∀x(x ∈ A
→ x ∈ B)
is true.
Theorem for Subsets :
For every set S,
For every set S,
The set A is a subset of B iff
every element of A is also an element of B.
We use the notation A ⊆ B to indicate
that A is a subset of the set B.
We see that A ⊆ B if and only if the
quantification ∀x(x ∈ A → x ∈ B)
is true.
The set A is a subset of B iff
every element of A is
also an element of B.
We use the notation A ⊆
B to indicate
that A is a subset of the set B.
We see that A ⊆ B if and only if the
quantification ∀x(x ∈
A → x ∈ B)
is true.
Let S be a set. If there are exactly n distinct elements in S where n is a nonnegative integer, we say that S is a finite set and that n is the cardinality of S. The cardinality of S is denoted by |S|.
Let S be a set. If there are
exactly n distinct elements in S where
n is a nonnegative integer, we say that
S is a finite set and that n is the cardinality
of S. The cardinality of S
is denoted by |S|.
Remark: The term cardinality
comes from the common usage of the
term cardinal number as the size of a finite set.
For Example: Let A be the
set of odd positive integers less than 10.
Then |A| = 5.
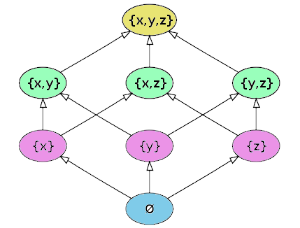
Given a set S, the power set of S is the set of all subsets of the set S. The power set of S is denoted by P(S).
Given a set S, the power set
of S is the set of
all subsets of the set S.
The power set of S is denoted
by P(S).
For Example:
If S is the set {x, y, z},
then the subsets of S are
{} (the empty set or the null set)
{x}
{y}
{z}
{x, y}
{x, z}
{y, z}
{x, y, z}
and hence the power set of S is {{},
{x}, {y}, {z},
{x, y},
{x, z}, {y, z},
{x, y, z}}.
Size of the power set of a set of size n
is 2n. Why? See
Pascal's Triangle
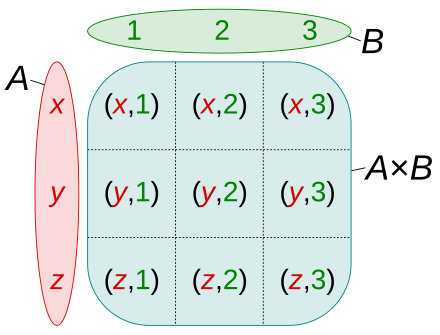
Let A and B be sets. The Cartesian product of A and B,
denoted by A x B, is the set of all ordered pairs (a, b),
where a ∈ A and b ∈ B. Hence,
A x B = {(a, b) | a ∈ A ∧ b ∈ B}.
The ordered n-tuple
(a1, a2, ... , an)
is the ordered collection that has a1 as
its first element,
a2 as its second element, ... ,
and an as its nth element.
In other words, (a1, a2,
... , an) =
(b1, b2, ... ,
bn) if and only if ai = bi,
for i = 1, 2, ... , n.
1. d; 2. a; 3. c; 4. c; 5. a;
Two, or more, sets can be combined in many different ways.
For instance, starting with the set of mathematics majors at
your school and the set of computer science majors at your school,
we can form the set of students who are mathematics majors or
computer science majors, the set of students who are joint
majors in mathematics and computer science, the set of
all students not majoring in mathematics, and so on.
Khan Academy on Set Operations
Two sets can be "added" together. The union of A and B, denoted by A ∪ B, is the set of all things that are members of either A or B.

Examples:
{1, 2} ∪ {1, 2} = {1, 2}.
{1, 2} ∪ {2, 3} = {1, 2, 3}.
{1, 2, 3} ∪ {3, 4, 5} = {1, 2, 3, 4, 5}
A new set can also be constructed by determining which members two sets have "in common". The intersection of A and B, denoted by A ∩ B, is the set of all things that are members of both A and B. If A ∩ B = ∅, then A and B are said to be disjoint.

Examples:
{1, 2} ∩ {1, 2} = {1, 2}.
{1, 2} ∩ {2, 3} = {2}.
Two sets can also be "subtracted". The relative complement of B in A (also called the set-theoretic difference of A and B), denoted by A − B, is the set of all elements that are members of A but not members of B.


In certain settings all sets under
discussion are considered
to be subsets of a given universal set U.
In such cases, U − A
is called the absolute complement or
simply complement of A, and is denoted
by an A with a bar over it.
For instance:
1. {1, 2} − {1, 2} = ∅.
2. {1, 2, 3, 4} − {1, 3} = {2, 4}.
Some basic properties of complements:
1. A − B
≠ B − A
for A ≠ B.
2. A ∪ A
= U.
3. A ∩ A
= ∅.
4. A = A.
5. A − A = ∅.
6. U = ∅
and ∅ = U.
7. A − B = A ∩
B.
The fundamental laws of set algebra :
If A and B are any two sets then,
There are various ways to represent sets using a computer.
One method is to store the elements of the set in an
unordered fashion. However:
Wastes time searching when doing union, intersection,
etc.
We can represent set by a bit string: bit x
is on if x is in the set.
For Example :
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10},
and the ordering of elements of U has
the elements in increasing
order; that is, ai = i.
What bit strings represent the subset of
all odd integers in U, the subset
of all even integers in U,
and the subset of integers not exceeding 5 in U?
Solution:
The bit string that represents the set of odd
integers in U, namely, {1, 3, 5, 7, 9},
is 10 1010 1010.
All even integers in U: 01 0101 0101.
1. c; 2. b; 3. a; 4. b; 5. b;
A function is a relation between a set of inputs
and a set of permissible outputs with the property that
each input is related to exactly one output.
Let A and B be nonempty sets.
A function f from
A to B is an assignment of exactly one element of
B to each element of A.
We write f(a) = b if b is
the unique element of B assigned by the function f
to the element a of A.
If f is a function from A to B,
we write f : A → B.

A function f is said to
be one-to-one, or an injunction,
if and only if f(a) = f(b)
implies that a = b for all a and b in the domain of f.
A function is said to be injective if it is one-to-one.
Note that a function f is one-to-one if and
only if f (a) ≠ f (b) whenever a ≠ b. This
way of expressing that f is one-to-one is obtained by
taking the contrapositive of the
implication in the definition.
For example:
Determine whether the function f
from {a, b, c, d} to {1, 2, 3, 4, 5}
with f(a) = 4, f(b) = 5,
f(c) = 1, and f(d) = 3 is one-to-one?
Answer: The function f is one-to-one because f takes
on different values at the four elements of its domain.
as
f(a) = 4, f(b) = 5, f(c) = 1, and f(d) = 3
A function f from A to B is
called onto, or a surjection, if and only if for every
element b ∈ B
there is an element a ∈
A with f(a) = b.
A function f from A to B is
called onto, or a surjection, if and only if for every
element b ∈ B
there is an element a ∈
A with f(a) = b.
A function f is called surjective if it is onto.
For Example: Is the function
f(x) = x + 1 from
the set of integers to the set of integers onto?
This function is onto, because for every
integer y there is an
integer x such that
f(x) = y.
To see this, note that
f(x) = y if and
only if x + 1 = y, which holds
if and only if x = y − 1.
The function
composition of two functions takes the output
of one function as the input of a second one. More
specifically, the composition
of f with a function
g: Y → Z is the function
(g º f:
X → Z) defined by
(g º f)(x)
= g(f(x)).
The order of the composition can be important.
For example, suppose
f(x) = x2
and g(x) = x + 1.
Then g(f(x))
= x2 + 1, while
f(g(x))
= (x + 1)2,
which is x2 + 2x + 1,
a different function.

Let f be a one-to-one correspondence from the set A to the set B. The inverse function of f is the function that assigns to an element b belonging to B the unique element a in A such that f(a) = b. The inverse function of f is denoted by f−1. Hence, f−1(b) = a when f(a) = b.
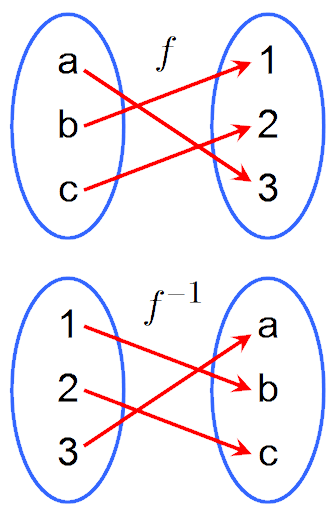
Because f maps a to 3, the inverse f−1 maps 3 back to a. This function is onto, because for every integer y there is an integer x such that f(x) = y. To see this, note that f(x) = y if and only if x + 1 = y, which holds if and only if x = y − 1.


Let x be a real number. The floor function rounds x down to the closest integer less than or equal to x, and the ceiling function rounds x up to the closest integer greater than or equal to x.

Let x be a real number. The floor function rounds x down to the closest integer less than or equal to x, and the ceiling function rounds x up to the closest integer greater than or equal to x.

1. b; 2. b; 3. c; 4. d; 5. c; 6. d;
A sequence is a function from a
subset of the set of integers (usually
either the set {0, 1, 2, ...}
or the set {1, 2, 3,...}) to a set S. We use the
notation an
to denote the image of the integer.
We call an a term of the sequence.
For Example: Consider the sequence {a}, where
a = 1/n
The list of the terms of this sequence,
beginning with a1,
namely, a1, a2,
a3, a4,...,
starts with
1, 1/2, 1/3, 1/4,....
1. a; 2. a; 3. d; 4. b; 5. b;
The sets A and B have the same cardinality if and only if there is a one-to-one correspondence from A to B. When A and B have the same cardinality, we write |A| = |B|.
If there is a one-to-one function from A to B, the cardinality of A is less than or the same as the cardinality of B and we write |A| ≤ |B|. Moreover, when |A| ≤ |B| and A and B have different cardinality, we say that the cardinality of A is less than the cardinality of B and we write |A| < |B|.
A set that is either finite or has the same
cardinality as the set of positive integers
is called countable. A set that is not
countable is called uncountable. When an infinite
set S is countable, we denote the cardinality of
S by ℵ0
(where ℵ is aleph, the first letter of
the Hebrew alphabet). We write |S|
= ℵ0
and say that S has cardinality "aleph null."
For Example:
Show that the set of all integers is countable.
Solution:
We can list all integers in a
sequence by starting with 0 and alternating between
positive and negative integers: 0, 1, -1, 2, -2, ...
Alternatively, we could find a one-to-one correspondence
between the set of positive integers and the set of
all integers.
The function f(n) = n/2
when n is even and
f(n) = -(n − 1)/2
when n is odd is such a function.
Consequently, the set of all integers is countable.
A surprising result:
The rational numbers are countable.
How do we order them?
All rational numbers p/q where p +
q add to 2, then all where they add to 3...
So...
1/1, 1/2, 2/1, 1/3, 3/1, 1/4, 2/3, 3/2, 4/1...
An uncountable set (or uncountably
infinite set) is an infinite set that
contains too many elements to be countable.
The uncountability of a set is closely related
to its cardinal number: a set is uncountable
if its cardinal number is larger than
that of the set of all natural numbers.
There is an injection from the smaller set to
the larger set, but no bijection.
1. a; 2. b; 3. b; 4. b; 5. b;
A matrix is a rectangular array of numbers.
A matrix with m rows and n columns is
called an m &mul; n matrix.
The plural of matrix is matrices. A matrix with the same
number of rows as columns is called square. Two matrices
are equal if they have the same number of rows and the same
number of columns and the corresponding
entries in every position are equal.





