
Combinatorics: Study of arangement of objects.
Enumeration: Counting of objects with certain properties.
Say we have a set of objects with certain properties.
Counting is used to determine the number of these objects.
Counting problems arise throughout
mathematics and computer science.
Examples:
1. The successful outcomes of experiments.
2. The number of operations used by an
algorithm: its time complexity.
There are two basic counting principles.
The Product Rule
Suppose that a procedure can be broken into two
parts, and there are n1 ways
to do the first part, and n2
ways to do the second (and the choices for the two
parts are independent). Then there are
n1n2 ways to do
the task.
Examples:
The procedure of labeling a chair
consists of two tasks, namely,
assigning to the seat one of the
26 uppercase English letters,
and then assigning to it
one of the 100 possible integers.
1. The chairs of an auditorium are to be
labeled with an uppercase English
letter followed by a positive
integer not exceeding 100.
What is the largest number of chairs
that can be labeled differently?
Answer:
The product rule shows that there are
26 * 100 = 2600
different ways that a chair can be labeled.
Therefore, the largest number of chairs
that can be
labeled differently is 2600.
There are 26 choices
for each of the three uppercase
English letters and ten choices
for each of the three digits.
Hence, by the product rule there are a total
of
2. How many different license plates
can be made if each plate contains a
sequence of three uppercase English letters
followed by three digits
(and no sequences of letters are prohibited,
even if they are obscene)?

Answer:
26 * 26 * 26 * 10 * 10 * 10 = 17,576,000
possible license plates.
The Sum Rule
If a task can be done in either one of
n1 ways or one of
n2 ways, then it can be done in
n1 + n2 ways.
Examples:
1. A student can choose a computer project
from one of three lists.
The three lists contain 23, 15, and
19 possible projects, respectively.
No project is on more than one list.
How many possible projects are there to choose from?
The student can choose a project
by selecting a project from the first list,
the second list, or the third list.
Because no project is on more than one list,
by the sum rule there are
23 + 15 + 19 = 57 ways
to choose a project.
2.What is the value of k after the following code, where n1, n2, . . . , nm are positive integers, has been executed?

The initial value of k is zero.
This block of code is made up of m different loops.
Each time a loop is traversed, 1 is added to k.
To determine the value of k
after this code has been executed,
we need to determine how
many times we traverse a loop.
Note that there are ni ways
to traverse the ith loop.
Because we only traverse one loop at a time,
the sum rule shows that the final value of k,
which is the number of ways to traverse
all of the m loops is:
n1 +
n2 + ...
+ nm
Example:
Each user on a computer system has a
password, which is six to eight characters long,
where each character is an uppercase letter or a digit.
Each password must contain at least one digit.
How many possible passwords are there?
Let P be the total number of possible passwords,
and let P6, P7,
and P8 denote the number of
possible passwords of length 6, 7, and 8, respectively.
By the sum rule, P =
P6 + P7 + P8.
We will now find P6 , P7,
and P8.
Finding P6
directly is difficult. To find P6
it is easier to find the number of strings of
uppercase letters and digits that are six characters long,
including those with no digits, and subtract from
this the number of strings with no digits.
By the product rule, the number of strings of
six characters is 366,
and the number of strings with no
digits is 266. Hence,
P6 =
366 - 266 =
2,176,782,336 - 308,915,776 = 1,867,866,560.
Similarly, we have
P7 =
367 - 267 =
78,364,164,096 - 8,031,810,176 = 70,332,353,920
and
P8 =
368 - 268 =
2,821,109,907,456 - 208,827,064,576 = 2,612,282,842,880.
P =
P6 + P7 + P8 =
2,684,483,063,360.
The Subtraction Rule
If a task can be done in n1 ways or
n2 ways, then the number of total ways it
can be done is n1 +
n2 minus the number of ways common to
n1 and n2.
Example:
A computer company receives 350 applications
from computer graduates for a job planning
a line of new web servers.
Suppose that 220 of these applicants
majored in computer science, 147 majored in business,
and 51 majored both in computer science and in business.
How many of these applicants majored neither
in computer science nor in business?
To find the number of these applicants who majored
neither in computer science nor in business, we
can subtract the number of students who majored
either in computer science or in business (or both)
from the total number of applicants.
Let A1 be the set of students who majored in
computer science and A2 the set of students
who majored in business.
Then A1 ∪
A2 is the
set of students who majored in
computer science or business (or both),
and A1 ∩
A2 is the set of students who
majored both in computer science and in business.
By the subtraction rule the number of students
who majored either in computer science
or in business (or both) equals:
|A1 ∪ A2|
= |A1 | + |A2|
- |A1 ∩ A2|
= 220 + 147 - 51 = 316.
We conclude that 350 - 316 = 34 of the applicants
majored neither in computer science nor in business.
The Division Rule
There are n / d ways to do a task
when it can be carried out in n ways, and for every
way w exactly d of the n
ways correspond to w.
Example:
How many different ways are
there to seat four people around a circular table,
where two seatings are considered the same
when each person has the same left neighbor
and the same right neighbor?
We arbitrarily select a seat at
the table and label it seat 1.
We number the rest of the seats in numerical order,
proceeding clockwise around the table.
Note that are four ways to select the person for seat 1,
three ways to select the person for seat 2,
two ways to select the person for seat 3,
and one way to select the person for seat 4.
Thus, there are 4! = 24 ways
to order the given four people for these seats.
However, each of the four choices for
seat 1 leads to the same arrangement,
as we distinguish two arrangements only
when one of the people has a different immediate
left or immediate right neighbor.
Because there are four ways to
choose the person for seat 1,
by the division rule there are 24/4 = 6
different seating arrangements of four
people around the circular table.
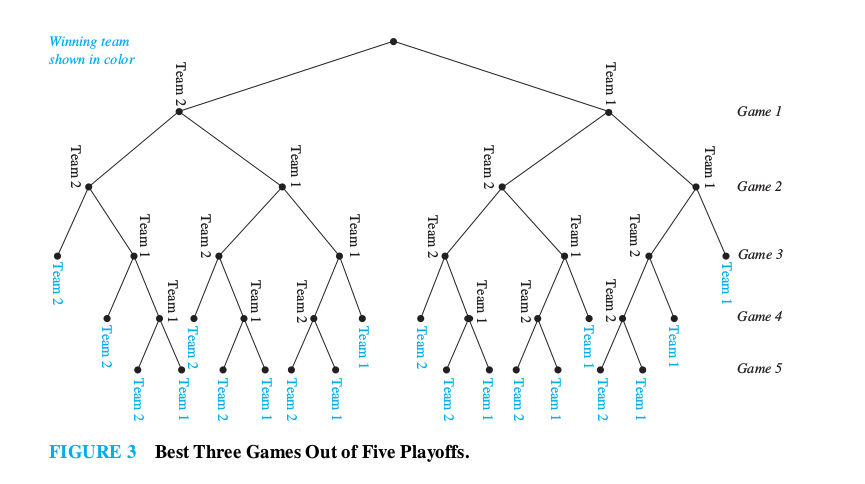
Example:
A playoff between two teams consists of at most five games.
The first team that wins three games wins the playoff.
In how many different ways can the playoff occur?
The tree diagram in Figure 3 displays
all the ways the playoff can proceed,
with the winner of each game shown.
We see that there are 20 different
ways for the playoff to occur.
1. a; 2. a; 3. c; 4. a; 5. b; 6. a;

The pigeonhole principle states that
if there are more pigeons than pigeonholes,
then there must be at least one pigeonhole
with at least two pigeons in it.
The Pigeonhole Principle
If k is a positive integer and k
+ 1 objects are to be placed into k
boxes, then at least one box must have more than
one object in it.
A function f from a set with k + 1 or more elements to a set with k elements is not one-to-one.
How many students must be in a class to guarantee that at least two students receive the same score on the final exam, if the exam is graded on a scale from 0 to 100 points?
There are 101 possible scores on the final. The pigeonhole principle shows that among any 102 students there must be at least 2 students with the same score.
The pigeonhole principle states that there must be at least two objects in the same box when there are more objects than boxes. However, even more can be said when the number of objects exceeds a multiple of the number of boxes. For instance, among any set of 21 decimal digits there must be 3 that are the same. This follows because when 21 objects are distributed into 10 boxes, one box must have more than 2 objects.
The Generalized Pigeonhole Principle
If n objects are placed into k
boxes, then there is at least one box containing at
least ceiling(n / k) objects.
What is the minimum number of students required in a discrete mathematics class to be sure that at least six will receive the same grade, if there are five possible grades, A, B, C, D, and F?
The minimum number of students needed to ensure that
at least six students receive the same grade is
the smallest integer n such that
ceiling(n / 5) = 6.
The smallest such integer is n = 5 * 5 + 1 = 26.
If you have only 25 students, it is possible for
there to be five who have received
each grade so that no six
students have received the same grade.
Thus, 26 is the minimum number of students needed to ensure
that at least six students will receive the same grade.
Assume that in a group of six people, each pair of
individuals consists of two friends or two enemies.
Show that there are either three mutual friends or
three mutual enemies in the group.
1. c; 2. a; 3. d; 4. a; 5. b;

A permutation of a set of distinct objects is an
ordered arrangement of these objects.
An ordered arrangement of r elements of a set is
called an r-permutation.

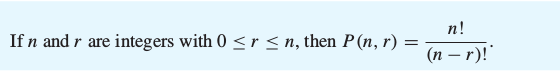
How many ways are there to select a first-prize winner,
a second-prize winner, and a third-prize winner
from 100 different people who have entered a contest?
P (100, 3) = 100 * 99 * 98 = 970,200
How many permutations of the letters ABCDEFGH
contain the string ABC ?
Because the letters ABC must occur as a block,
we can find the answer by finding the number of permutations
of six objects, namely, the block ABC and the
individual letters D, E, F , G, and H .
Because these six objects can occur in any order,
there are 6! = 720 permutations of the
s letters ABCDEFGH in which ABC occurs as a block.
An r-combination of elements of a set is an
unordered selection of r elements from the set.
Thus, an r-combination is simply a subset of the
set with r elements.
The number of r-combinations of a set with n
distinct elements is denoted by C(n, r).
C(n, r) is called a binomial coefficient.

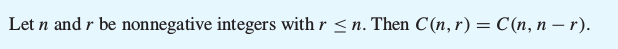

How many ways are there to select five players from a
10-member tennis team to make a trip
to a match at another school?
C(10, 5) = 10! /( 5! * 5!) = 252
How many bit strings of length n contain
exactly r 1s?
The positions of r 1s in a bit
string of length n form
an r-combination of the set {1, 2, 3, . . . , n}.
Hence, there are C(n, r)
bit strings of length n
that contain exactly r 1s..
1. a; 2. d; 3. a; 4. b; 5. d;
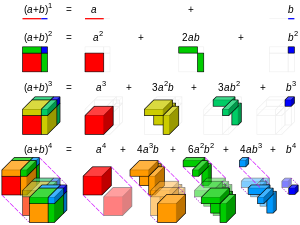
The binomial theorem gives the coefficients of the
expansion of powers of binomial expressions.
A binomial expression is simply the sum of two terms, such as x + y.
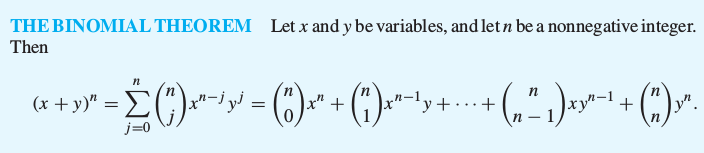






More on Pascal's triangle
Khan Academy video on Pascal's triangle



How many strings of length r can be formed
from the uppercase letters of the English alphabet?
By the product rule, because there are 26 uppercase English letters,
and because each letter can be used repeatedly,
we see that there are 26 r strings of
uppercase English letters of length r.
The number of r-permutations of a set with n elements when
repetition is allowed is given in Theorem 1.
Suppose that a cookie shop has four different kinds of cookies.
How many different ways can six cookies be chosen?
Assume that only the type of cookie,
and not the individual cookies or the order
in which they are chosen, matters.
The number of ways to choose six cookies is
the number of 6-combinations of a set with four elements.
From Theorem 2 this equals C(4 + 6 - 1, 6) = C(9, 6).
C(9, 6) = C(9, 3) = (9 * 8 * 7) / (1 * 2* 3) = 84
There are 84 different ways to choose the six cookies.
Every sequence of n2 + 1 distinct numbers must contain a sequence of length n + 1 that is either strictly increasing or strictly decreasing.
How many different strings can be made by
reordering the letters of the word SUCCESS?
Because some of the letters of SUCCESS are the same,
the answer is not given by the number of permutations of seven letters.
This word contains three Ss, two Cs, one U , and one E.
To determine the number of different strings
that can be made by reordering the letters, first note that
the three Ss can be placed among
the seven positions in C(7, 3) different ways,
leaving four positions free.
Then the two Cs can be placed in C(4, 2) ways,
leaving two free positions. The U can be placed in C(2, 1) ways,
leaving just one position free. Hence E can be placed in C(1, 1) way.
Consequently, from the product rule,
the number of different strings that can be made is
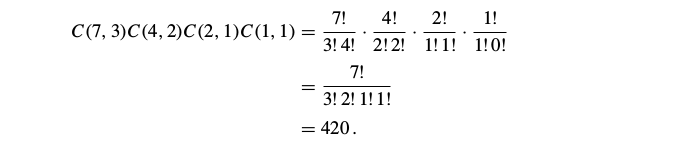
Example:
How many ways are there to distribute hands of 5 cards
to each of four players from the standard deck of 52 cards?

Counting the number of ways of placing n
indistinguishable objects into k distinguishable
boxes turns out to be the same as counting the
number of n-combinations for a set with k elements
when repetitions are allowed.
The reason behind this is that there is a
one-to-one correspondence between n-combinations
from a set with k elements when repetition
is allowed and the ways to place n indistinguishable
balls into k distinguishable boxes.
To set up this correspondence, we put
a ball in the ith bin each time
the ith element of the set is
included in the n-combination.
Example:
How many ways are there to place 10
indistinguishable balls into eight distinguishable bins?
Counting the ways to place n distinguishable objects into k indistinguishable boxes is more difficult than counting the ways to place objects, distinguishable or indistinguishable objects, into distinguishable boxes.
Example:
How many ways are there to put four different employees into
three indistinguishable offices, when each office can
contain any number of employees?
Some counting problems can be solved by determining the number of ways
to distribute indistinguishable objects into indistinguishable boxes.
We illustrate this principle with an example.
Example:
How many ways are there to pack six copies of the same book
into four identical boxes, where a box can contain as many as six books?

Generate the permutations of the integers 1, 2, 3
in lexicographic order.
Begin with 123.
The next permutation is obtained by interchanging 3 and 2 to obtain 132.
Next, because 3 > 2 and 1 < 3, permute the three integers in 132.
Put the smaller of 3 and 2 in the first position, and
then put 1 and 3 in increasing order in positions 2 and 3 to obtain 213.
This is followed by 231, obtained by interchanging 1 and 3, because 1 < 3.
The next larger permutation has 3 in the first position,
followed by 1 and 2 in increasing order, namely, 312.
Finally, interchange 1 and 2 to obtain the last permutation, 321.
We have generated the permutations of 1, 2, 3 in lexicographic order.
They are 123, 132, 213, 231, 312, and 321.

Find the next bit string after 10 0010 0111.
The first bit from the right that is not a 1 is
the fourth bit from the right.
Change this bit to a 1 and change all the following bits to 0s.
This produces the next larger bit string, 10 0010 1000.

Find the next larger 4-combination of the set
{1, 2, 3, 4, 5, 6} after {1, 2, 5, 6}.
The last term among the terms ai with a1= 1, a2 = 2, a3 = 5, and a4 = 6 such that ai ≠ 6 − 4 + i is a 2 = 2.
To obtain the next larger 4-combination, increment a2 by 1 to obtain a2 = 3. Then set a3 = 3 + 1 = 4 and a4 = 3 + 2 = 5.
Hence the next larger 4-combination is {1, 3, 4, 5}.