

Definition 1:
A graph G = (V, E)
consists of V,
a nonempty set of vertices (or nodes) and E,
a set of edges. Each edge has either one or
two vertices associated with it,
called its endpoints. An edge is said
to connect its endpoints.
Definition 2:
A directed graph (or digraph) (V,
E) consists of a nonempty set of vertices V
and a set of directed edges (or arcs) E.
Each directed edge is associated with
an ordered pair of vertices.
The directed edge associated with the ordered pair
(u, v) is said to start at
u and end at v.
| Type | Edges | Multiple Edges Allowed
Between Two Vertices? |
Loops Allowed? |
|---|---|---|---|
| Simple Graph | Undirected | No | No |
| Multigraph | Undirected | Yes | No |
| Pseudograph | Undirected | Yes | Yes |
| Simple Directed Graph | Directed | No | No |
| Directed Multigraph Graph | Directed | Yes | Yes |
| Mixed Graph | Directed and Undirected | Yes | Yes |
Examples: Acquaintanceship (Friendship Graphs), Influence Graphs, Collaboration Graphs.

Examples: Call Graphs
Examples: The Web Graph, Citation Graphs.
Examples: Module Dependency Graphs, Precedence Graphs and Concurrent Processing.
Examples: Airline Routes, Road Networks.

Examples: Niche Overlap Graphs in Ecology, Protein Interaction Graphs.
Examples: Round-Robin Tournaments, Single-EliminationTournaments.
Two vertices u and v in an undirected graph G are called adjacent (or neighbors) in G if u and v are endpoints of an edge e of G. Such an edge e is called incident with the vertices u and v and e is said to connect u and v.
The set of all neighbors of a vertex v of G = (V, E), denoted by N(v), is called the neighborhood of v. If A is a subset of V, we denote by N(A) the set of all vertices in G that are adjacent to at least one vertex in A. So, N(A) = ∪v ∈ A N(v).
The degree of a vertex in an undirected graph is the number of edges incident with it, except that a loop at a vertex contributes twice to the degree of that vertex. The degree of the vertex v is denoted by deg(v).
The Handshaking Theorem:
Let G = (V, E)
be an undirected graph with m
edges. Then
2m = ∑
v ∈ V
deg(v).
(Note that this applies even if multiple
edges and loops are present.)
An undirected graph has an even number
of vertices of odd degree.
Let's try proving this by induction.
When (u, v) is an edge of the graph G with directed edges, u is said to be adjacent to v and v is said to be adjacent from u. The vertex u is called the initial vertex of (u, v), and v is called the terminal or end vertex of (u, v). The initial vertex and terminal vertex of a loop are the same.
In a graph with directed edges the
in-degree of a vertex v,
denoted by deg-(v), is the number
of edges with v as their terminal vertex.
The out-degree of v,
denoted by deg+(v), is the
number of edges with v as their initial vertex.
(Note that a loop at a vertex contributes 1 to
both the in-degree and the out-degree of this vertex.)
Let G = (V, E) be a graph
with directed edges. Then
∑v ∈ V
deg-(v) =
∑v ∈ V
deg+(v) = |E|
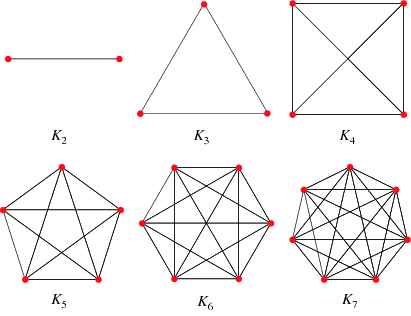
A complete graph on n vertices,
denoted by Kn, is a simple graph
that contains exactly one edge between
each pair of distinct vertices.
A simple graph for which there is at least one
pair of distinct vertex not connected
by an edge is called noncomplete.

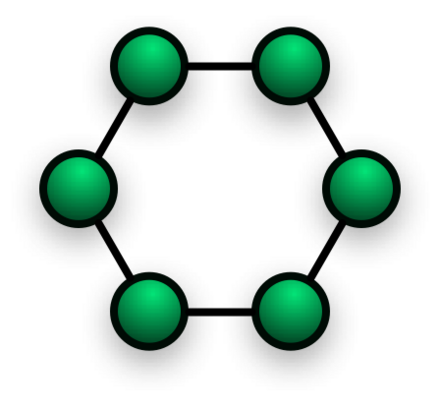
A cycle Cn, n ≥ 3, consists of n vertices v1, v2,..., vn and edges {v1, v2}, {v2, v3}, ..., {vn−1, vn}, and {vn, v1}.

We obtain a wheel Wn when we add an additional vertex to a cycle Cn, for n ≥ 3, and connect this new vertex to each of the n vertices in Cn, by new edges.
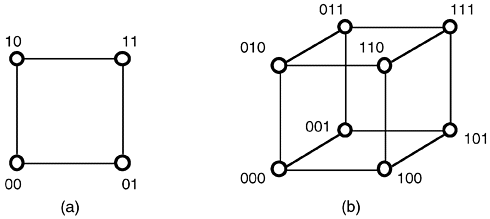
An n-dimensional hypercube, or n-cube, denoted by Qn, is a graph that has vertices representing the 2n bit strings of length n. Two vertices are adjacent if and only if the bit strings that they represent differ in exactly one bit position.
A simple graph G is called bipartite if its vertex set V can be partitioned into two disjoint sets V1 and V2 such that every edge in the graph connects a vertex in V1 and a vertex in V2 (so that no edge in G connects either two vertices in V1 or two vertices in V2). When this condition holds, we call the pair (V1, V2) a bipartition of the vertex set V of G.
A simple graph is bipartite if and only if it is possible to assign one of two different colors to each vertex of the graph so that no two adjacent vertices are assigned the same color.
Definition:
A matching is a set of edges without common vertices.
Theorem 5:
HALL'S MARRIAGE THEOREM
The bipartite graph G =
(V, E) with bipartition
(V1, V2) has
a complete matching from
V1 to
V2 if and only if
|N(A)| ≥ |A| for all subsets
A of V1.
(N(A) is the neighborhood of A.)

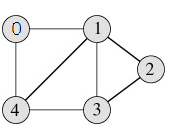
A subgraph of a graph G = (V, E) is a graph H = (W, F), where W ⊆ V and F ⊆ E. A subgraph H of G is a proper subgraph of G if H ≠ G.
Let G = (V, E) be a simple graph. The subgraph induced by a subset W of the vertex set V is the graph (W, F) where the edge set F contains an edge in E if and only if both endpoints of this edge are in W.
The union of two simple graphs G1 = (V1, E1) and G2 = (V2, E2) is the simple graph with vertex set V1 ∪ V2 and edge set E1 ∪ E2. The union of G1 and G2 is denoted by G1 ∪ G2.

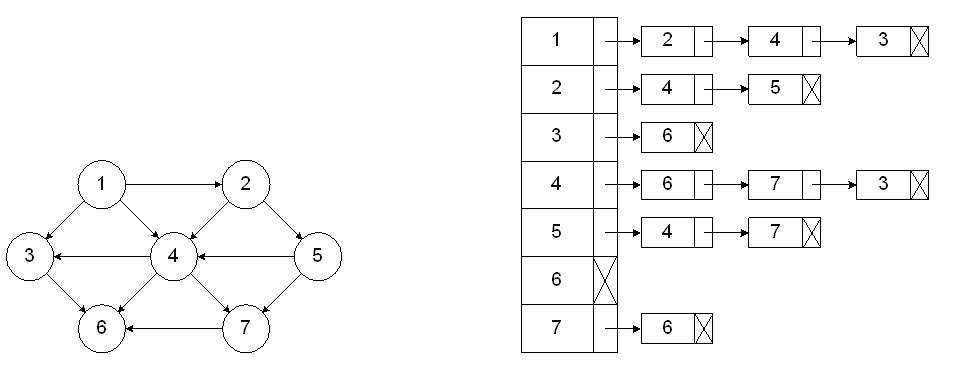

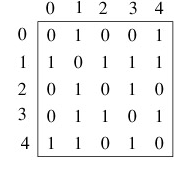
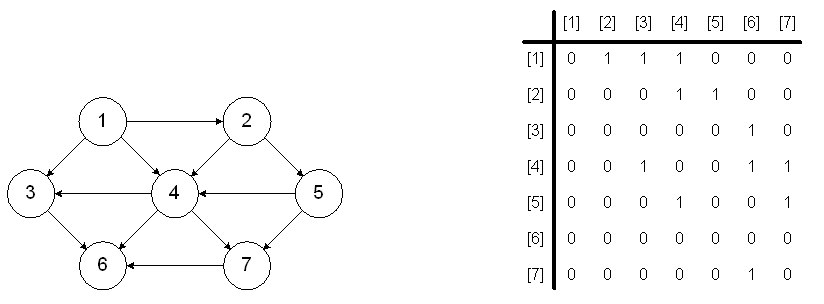
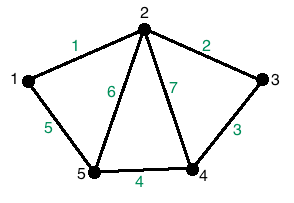
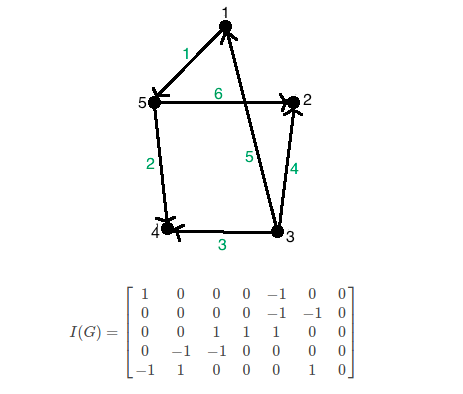
Let G = (V, E)
be an undirected graph.
Suppose that v1,
v2,...,
vn are the vertices
and e1,
e2, ...,
em are the edges
of G. Then the incidence
matrix with respect to this
ordering of V and E
is the n x m matrix
M = [mij], where
mij = 1
when edge ej
is incident with vi,
mij = 0 otherwise.
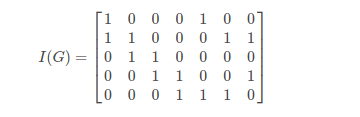
Definition 1:
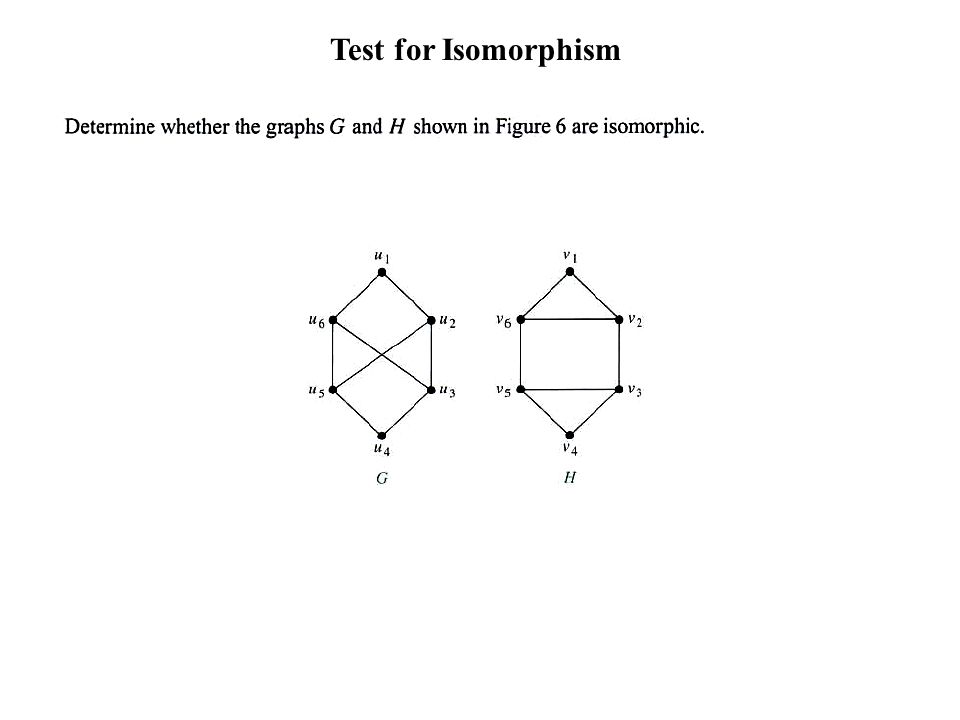
The simple graphs G1 = (V1, E1) and G2 = (V2, E2) are isomorphic if there exists a one-to-one and onto function f from V1 to V2 with the property that a and b are adjacent in G1 if and only if f(a) and f(b) are adjacent in G2, for all a and b in V1. Such a function f is called an isomorphism. Two simple graphs that are not isomorphic are called nonisomorphic.
It is difficult to show that two graphs are isomorphic. There are many possible one to one correspondences between the vertex sets of two simple graphs. There are n! possible mappings for graph with n vertices.
Instead of testing for each correspondence, we can show that two graphs are not isomorphic. If we can find only one property that only one of the two graphs has, then we can prove that the graphs are not isomorphic

A path through a graph is a sequence
of edges, starting at some vertex and moving
from vertex to vertex along edges.
A simple path cannot contain any edge
more than once.
Erdös number
Bacon number
Erdös-Bacon number
Collaboration graph of UGa math department

A graph is connected if there is a path from any vertex to any other vertex.
A connected component of a graph is a connected subgraph that is not a proper subgraph of another connected component.
Cut vertices or articulation points
Vertex cuts or separating sets
Edge cuts
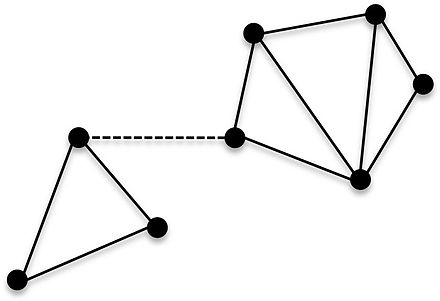
The edge connectivity of a graph is its minimum edge cut size.
Definition 4:
A directed graph is strongly connected if there is a path from a to b and from b to a whenever a and b are vertices in the graph
Definition 5:
A directed graph is weakly connected if there is a path between every two vertices in the underlying undirected graph
Paths and circuits can help in determining isomorphism.Length of circuit is a useful invariant in determining the isomorphism of two graphs. Also mappings constructed using paths can help in detecting isomorphism or its lack.
Can one take a walk that crosses each bridge in Königsberg once and only once?
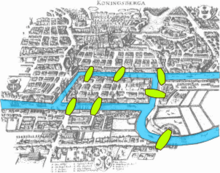
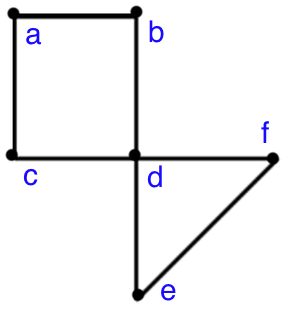
Answer: No! For an Eulerian path to exist through a graph, there must be zero or two nodes of odd degree.

For there to be an Eulerian circuit, all
nodes must have even degree. That is both
a necessary and a sufficient condition.
This can be proved with a graph like the following:
A simple path that passes through each vertex in a graph just once is called a Hamilton path. A simple circuit that passes through each vertex in a graph just once is called a Hamilton circuit.

There is no easy way to always detect Hamilton circuits, but... a graph with a Hamilton circuit:
Traveling salesperson problem (see below).
Gray codes

Introduce weighted graphs.
Discovered by Edsger Dijkstra.

1 function Dijkstra(Graph, source):
2
3 create vertex set Q
4
5 for each vertex v in Graph: // Initialization
6 dist[v] = INFINITY // Unknown distance from source to v
7 prev[v] = UNDEFINED // Previous node in optimal path from source
8 add v to Q // All nodes initially in Q
//(unvisited nodes)
9
10 dist[source] = 0 // Distance from source to source
11
12 while Q is not empty:
13 u = vertex in Q with min dist[u] // Node with the least distance
14 // will be selected first
15 remove u from Q
16
17 for each neighbor v of u: // where v is still in Q.
18 alt = dist[u] + length(u, v)
19 if alt < dist[v]: // A shorter path to v has been found
20 dist[v] = alt
21 prev[v] = u
22
23 return dist[], prev[]
Run-time analysis: at most n iterations of outer loop.
At most n - 1 iterations of inner loop.
So we are O(n2).
How to route our salesperson around their 10
stops at minimum cost?
Equivalent to finding all Hamiltonian circuits
starting at City 1.
That number will be (n - 1)! / 2,
which grows very fast.
For 12 cities, it will be around
20 million circuits
to try.
For 16 cities, it is approaching
1 trillion circuits!
r: # regions (or faces)
v: # vertices
e: # edges
Euler's formula:
r = e - v + 2
Also rendered as:
v - e + f = 2

CORROLARY 1:
If G(V, E)
is a connected planar graph and |V| > 2,
then |E| ≤ 3|V| - 6.
Show K5 is not planar.
A tournament is a directed graph (digraph) obtained by assigning a direction for each edge in an undirected complete graph.