

Mathematical induction can be used to prove statements that assert that P(n) is true for all positive integers n, where P(n) is a propositional function
PRINCIPLE OF MATHEMATICAL INDUCTION
To prove that P(n) is true for all positive integers n, where P(n) is a propositional function, we complete two steps :
BASIC STEP:
We verify that P(1) is true.
INDUCTIVE STEP:
We show that the conditional statement P(k) → P(k + 1) is true for all positive integers k.
Expressed as a rule of inference,
this proof technique can be stated as
(P(1) ∧ ∀k(P(k) →
P(k + 1))) → ∀nP(n),
when the domain is the set of positive integers.
The reason comes from the
well-ordering property.
To show: Mathematical Induction is valid.
Proved Facts: P(1) is true and
P(k) implies P(k + 1) is true
for all positive integers.
Assumption: There is at least one positive
integer for which P(n) is false.
Proof:
Then the set S of positive integers for which
P(n) is false is nonempty. Thus, by the
well-ordering property, S has a least element,
which will be denoted by m.
m
cannot be 1, because P(1) is true
Because m is positive and greater than 1,
m − 1 is a positive integer.
Furthermore, because m − 1 is
less than m, it is not in S,
so P(m − 1) must be true.
Because the conditional statement P(m − 1)
→ P(m) is also true, it must be the case
that P(m) is true. This contradicts the
choice of m).
Hence, P(n) must be true
for every positive integer n.
Good: it can be used to prove
a conjecture once it is has been made (and is true).
Bad:
It cannot be
be used to find new theorems.
Mathematicians sometimes find
proofs by mathematical induction
unsatisfying because they
do not provide insights as to why
theorems are true. Many
theorems can be proved in many ways,
including by mathematical
induction. Proofs of these theorems
by methods other than
mathematical induction are often preferred
because of the insights
they bring.
Show that if n is a positive integer, then 1 + 2 + . . . + n = n(n+1) ⁄ 2
BASIS STEP:
P(1) is true, because 1 = 1(1+1) ⁄ 2
INDUCTIVE STEP:
P(k) holds for an arbitrary
positive integer k.
we assume that 1 + 2 + . . . + k =
k(k+1)
⁄
2
Under this assumption,
it must be shown that P(k + 1) is true,
namely, that
1 + 2 + . . . + k + (k + 1) =
(k + 1)[(k + 1) + 1]
⁄
2
(k + 1)(k + 2)
⁄
2
is also true. When we add k + 1 to both sides of
the equation in P(k), we obtain
1 + 2+. . .+ k + (k + 1) =
k(k+1)
⁄
2
+
(k + 1)
=
k(k + 1) + 2(k + 1)
⁄
2
=
(k + 1)(k + 2)
⁄
2
This last equation shows that P(k + 1)
is true under the assumption that P(k) is true.
Use mathematical induction to prove the inequality
n < 2n
for all positive integers n.
BASIS STEP:
P(1) is true, because 1 < 21 = 2. This completes the basis step.
INDUCTIVE STEP:
We first assume the inductive hypothesis
that P(k) is true for an arbitrary
positive integer k. That is,
the inductive hypothesis P(k) is
the statement that k <
2k.
We need to show that if P(k) is true,
then P(k + 1), which is the statement
that k + 1 <
2k+1, is true.
That is, we need to show that if
k < 2k,
then k + 1 <
2k+1.
k + 1 < 2k
+ 1 ≤ 2k
+ 2k = 2 .
2k
= 2k + 1.
This shows that P(k + 1)
is true, namely,
that k + 1 <
2k+1,
based on the assumption that P(k)
is true.
Use mathematical induction to prove that n3 − n is divisible by 3 whenever n is a positive integer.
BASIS STEP:
The statement P(1) is true because 13 − 1 = 0 is divisible by 3.
INDUCTIVE STEP:
Assume that P(k) is true; that is, we
assume that k3 − k is
divisible by 3 for an arbitrary
positive integer k
(k + 1)3 − (k + 1)
= (k3 + 3k2 +
3k + 1) − (k + 1)
= (k3 − k)
+ 3(k2 + k).
Using the inductive hypothesis,
we conclude that the first
term k3 − k
is divisible by 3.
The second term is divisible by 3 because
it is 3 times an integer.
So, (k + 1)3 − (k + 1)
is also divisible by 3.
The Number of Subsets of a Finite Set
Use mathematical induction to show that if S is a
finite set with n elements,
where n is a nonnegative integer,
then S has 2n subsets.
Let P(n) be the proposition that a set
with n elements has 2n subsets.
BASIS STEP:
P(0) is true, because a set with zero elements, the empty set, has exactly 20 = 1 subset, namely, itself.
INDUCTIVE STEP:
P(k) is true for an arbitrary
nonnegative integer k, that is,
we assume that every set with
k elements has 2k subsets
Let T be a set with k + 1 elements.
It is possible to write
T = S ∪ {a},
where a is one of the elements of
T and S = T − {a}
(and hence |S| = k).
The subsets of T can be obtained in
the following way.
For each subset X of S there are
exactly two subsets of T ,
namely, X and X ∪ {a}.
These constitute all the subsets
of T and are all distinct.
S has 2k subsets,
because it has k elements.
We also know that there are two
subsets of T for each subset of S.
Therefore, there are 2 . 2k
= 2k+1
subsets of T. This finishes
the inductive argument.
P(n) is true for all nonnegative
integers n. That is, we have proved
that a set with n elements
has 2n
subsets whenever n is a
nonnegative integer.
NOTE: This is Pascal's Triangle showing up
again!
Here we will discuss the greedy scheduling algorithm.
Not covered for Fall 2017
Template for Proofs by Mathematical Induction
1. a; 2. d; 3. b;
To prove that P(n) is true for all positive integers n, where P(n) is a propositional function, we complete two steps:
BASIC STEP:
We verify that the proposition P(1) is true.
INDUCTIVE STEP:
We show that the conditional statement [P(1) ∨ P(2) ∨ . . . ∨ P(k)] → P(k + 1) is true for all positive integers k.
Show that if n is an integer greater than 1, then n can be written as the product of primes.
BASIC STEP:
P(2) is true, because 2 can be written as the product of one prime, itself.
INDUCTIVE STEP:
The inductive hypothesis is the
assumption that P(j) is true for all
integers j with 2 ≤
j ≤ k, that is,
the assumption that j can be written
as the product of primes
whenever j is a positive integer
at least 2 and not exceeding k.
There are two cases to consider,
namely, when k + 1 is prime and when
k + 1 is composite.
If k + 1 is prime, we immediately see
that P(k + 1) is true. Otherwise,
k + 1 is composite and
can be written as the product of two
positive integers a and b with
2 ≤ a ≤ b < k + 1.
Because both a and b are integers at
least 2 and not exceeding k, we can use
the inductive hypothesis to
write both a and b as the product of
primes. Thus, if k + 1 is composite, it
can be written as the
product of primes, namely,
those primes in the factorization
of a and those in the factorization
of b.
Hence, every nonnegative integer can
be written uniquely as the product of primes
in nondecreasing order.
Not covered for Spring 2018
Not covered for Spring 2018

We use two steps to define a function with the set of nonnegative integers as its domain.
BASIC STEP:
Specify the value of the
function at zero.
RECURSIVE STEP:
Give a rule for finding its
value at an integer from its
values at smaller integers.
Suppose that f is defined
recursively by
Example
f(0) = 3,
f(n + 1) = 2f(n) + 3.
Find f(1), f(2), f(3),
and f(4).
Solution:
From the recursive definition it
follows that
f(1) = 2f(0) + 3 =
2 * 3 + 3 = 9,
f(2) = 2f(1) + 3 =
2 * 9 + 3 = 21,
f(3) = 2f(2) + 3 =
2 * 21 + 3 = 45,
f(4) = 2f(3) + 3 =
2 * 45 + 3 = 93.
In the basis step, an initial collection
of elements is specified.
In the recursive step,
rules for forming new elements in the set from
those already known to be in the set are provided.
Recursive definitions may also include an exclusion
rule, which specifies that a recursively defined set
contains nothing other than those elements specified
in the basis step or generated by applications of the
recursive step.
The set ∑* of strings over the alphabet ∑ is defined recursively by
BASIS STEP:
λ ∈ ∑* (where λ is the empty string containing no symbols).
RECURSIVE STEP:
If w ∈ ∑* and x ∈ ∑, then wx ∈ ∑*.
Two strings can be combined via the operation of concatenation. Let ∑ be a set of symbols and ∑* the set of strings formed from symbols in ∑. We can define the concatenation of two strings, denoted by ·, recursively as follows.
BASIS STEP:
If w ∈ ∑*, then w · λ = w, where λ is the empty string.
RECURSIVE STEP:
If w1 ∈ ∑* and w2 ∈ ∑* and x ∈ ∑, then w1 · (w2x) = (w1 · w2)x.
Example:
Give a recursive
definition of l(w), the length
of the string w.
The length of a string can be
recursively defined by
l(λ) = 0;
l(wx) =
l(w) + 1 if w
∈ ∑*
and x ∈ ∑.
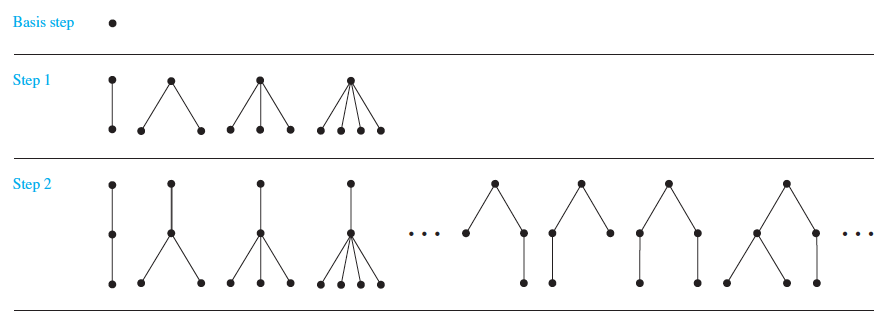
The set of rooted trees, where a rooted tree consists of a set of vertices containing a distinguished vertex called the root, and edges connecting these vertices, can be defined recursively by these steps:
BASIC STEP:
A single vertex r is a rooted tree.
RECURSIVE STEP:
Suppose that T1,
T2,
. . ., Tn are disjoint
rooted trees with roots
r1,
r2, . . . ,
rn, respectively.
Then the graph formed
by starting with a
root r, which is not
in any of the rooted
trees T1,
T2,
. . . , Tn,
and adding an edge from
r to each of the vertices
r1, r2,
. . . , rn,
is also a rooted tree.

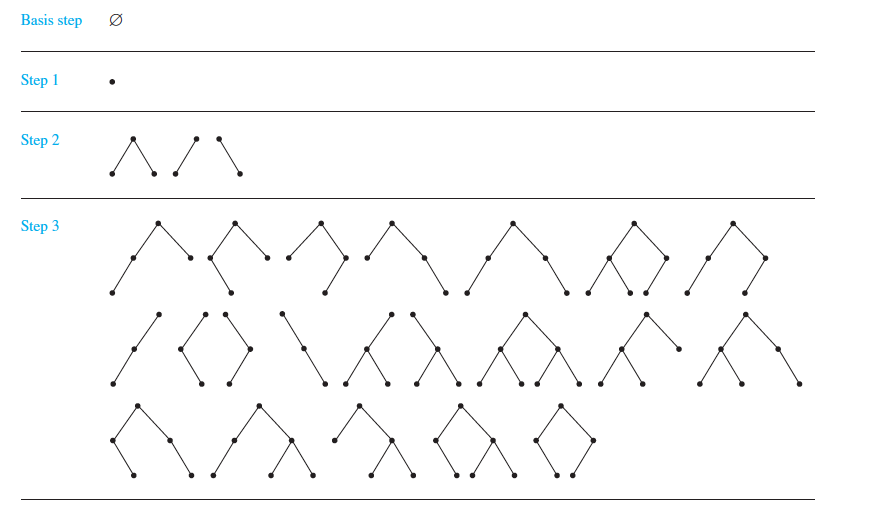
The set of extended binary trees can be defined recursively by these steps:
BASIC STEP:
The empty set is an extended binary tree.
RECURSIVE STEP:
If T1
and T2 are disjoint
extended binary trees,
there is an extended
binary tree, denoted by T1
· T2,
consisting of a root r
together with edges connecting
the root to each of the roots
of the left subtree
T1 and
the right subtree T2 when
these trees are nonempty.
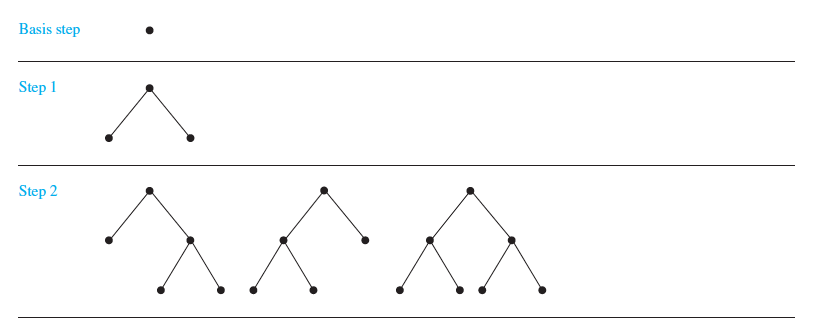
The set of full binary trees can be defined recursively by these steps:
BASIC STEP:
There is a full binary tree consisting only of a single vertex r.
RECURSIVE STEP:
If T1 and T2 are disjoint full binary trees, there is a full binary tree, denoted by T1 * T2, consisting of a root r together with edges connecting the root to each of the roots of the left subtree T1 and the right subtree T2.
We define the height h(T) of a full binary tree T recursively.
BASIC STEP:
The height of the full binary tree T consisting of only a root r is h(T) = 0.
RECURSIVE STEP:
If T1 and T2 are full binary trees, then the full binary tree v = T1 * T2 has height h(T ) = 1 + max(h(T1), h(T2)).
An algorithm is called recursive if it solves a problem by reducing it to an instance of the same problem with smaller input.
Give a recursive algorithm for computing n!, where n is a nonnegative integer.

Give a recursive algorithm for computing an, where a is a nonzero real number and n is a nonnegative integer.
Give a recursive algorithm for computing the greatest common divisor of two nonnegative integers a and b with a < b.

Devise a recursive algorithm for computing bn mod m, where b, n, and m are integers with m ≤ 2, n ≥ 0, and 1 ≤ b < m.

Express the linear search algorithm as a recursive procedure.
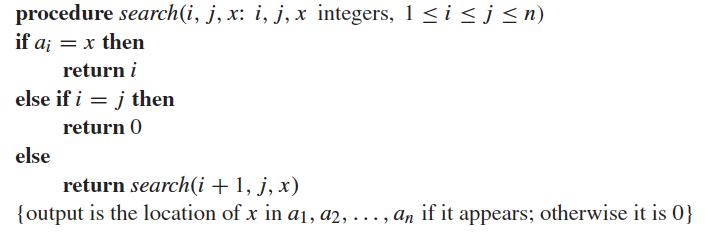
Construct a recursive version of
a binary search algorithm.

Instead of successively
reducing the computation
to the evaluation of the
function at smaller integers,
we can start with the value
of the function at one or
more integers, the base cases,
and successively apply the
recursive definition to
find the values of the function
at successive larger integers.
Such a procedure is
called iterative.


A Recursive Merge Sort.

Merging Two lists

A program is said to be
correct if it produces the
correct output for every
possible input. A proof
that a program is correct
consists of two parts.
The first part shows that
the correct answer is
obtained if the program
terminates. This part of
the proof establishes the
partial correctness
of the program.
The second part of the proof shows
that the program always terminates.
To specify what it means
for a program to produce
the correct output, two propositions
are used.
The first is the
initial assertion, which
gives the properties that the
input values must have.
The second is the final
assertion, which gives the properties
that the output of the program should
have, if the program
did what was intended.
A program, or program segment, S is said to be partially correct with respect to the initial assertion p and the final assertion q if whenever p is true for the input values of S and S terminates, then q is true for the output values of S. The notation p{S}q indicates that the program, or program segment, S is partially correct with respect to the initial assertion p and the final assertion q.
Not covered for Spring 2018
Not covered for Spring 2018