Number Theory and Cryptography

Action of the modular group on the upper-half plane
Divisibility and Modular Arithmetic

Division:
If a and b are integers with a ≠ 0, we say that a divides b if there is an integer c such that b = ac, or equivalently, if b/a is an integer. When a divides b we say that a is a factor.


Modular Arithmetic: If a and b are integers and m is a positive integer, then a is congruent to b modulo m if m divides a − b. We use the notation a ≡ b (mod m) to indicate that a is congruent to b modulo m. We say that a ≡ b (mod m) is a congruence and that m is its modulus (plural moduli). If a and b are not congruent modulo m, we write a ≢ b (mod m).

Modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" upon reaching a certain value -- the modulus (plural moduli)

Theorems
  1. Let a, b, and c be integers, where a ≠ 0. Then
    (i) if a | b and a | c, then a | (b + c);
    (ii) if a | b,then a | bc for all integers c;
    (iii) if a | b and b | c, then a | c.
  2. THE DIVISION ALGORITHM Let a be an integer and d a positive integer. Then there are unique integers q and r, with 0 ≤ r < d, such that a = dq + r.
  3. Let a and b be integers, and let m be a positive integer. Then a ≡ b (mod m) if and only if a mod m = b mod m.
  4. Let m be a positive integer. The integers a and b are congruent modulo m if and only if there is an integer k such that a = b + km
  5. Let m be a positive integer. If a ≡ b (mod m) and c ≡ d (mod m), then a + c ≡ b + d (mod m) and ac ≡ bd (mod m).

Corollary: 1. If a, b, and c are integers, where a ≠ 0, such that a | b and a | c, then a | mb + nc whenever m and n are integers.
2. Let m be a positive integer and let a and b be integers. Then (a + b) mod m = ((a mod m) + (b mod m)) mod m and ab mod m = ((a mod m)(b mod m)) mod m.

Integer Representations and Algorithms
NOT COVERED SPRING 2018

The most common representation of a positive integer is a string of bits, using the binary numeral system. The order of the memory bytes storing the bits varies; see endianness. The width or precision of an integral type is the number of bits in its representation. An integral type with n bits can encode 2n numbers; for example an unsigned type typically represents the non-negative values 0 through 2n − 1. Other encodings of integer values to bit patterns are sometimes used, for example Binary-coded decimal or Gray code, or printed character codes such as ASCII.

Theorem 1
  1. Let b be an integer greater than 1. Then if n is a positive integer, it can be expressed uniquely in the form
    n = akbk + ak-1bk-1 + ‧‧‧ + a1b + a0,
    where k is a nonnegative integer, a0, a1, ... , ak are non-negative integers less than b, and ak ≠ 0.
Algorithms for Integer Operations

The algorithms for performing operations with integers using their binary expansions are extremely important in computer arithmetic.

We will describe algorithms for the addition and the multiplication of two integers expressed in binary notation.

Types of Algorithms
  1. ADDITION ALGORITHM: Consider the problem of adding two integers in binary notation. A procedure to perform addition can be based on the usual method for adding numbers with pencil and paper. This method proceeds by adding pairs of binary digits together with carries, when they occur, to compute the sum of two integers.
    Example:Add a = (1110)2 and b = (1011)2
    Solutions: Following the procedure specified in the algorithm, first note that
    a0 + b0 = 0 + 1 = 0 × 2 + 1,
    so that c0 = 0 and s0 = 1. Then, because
    a1 + b1 + c0 = 1 + 1 + 0 = 1 × 2 + 0,
    it follows that c1 = 1 and s1 = 0. Continuing,
    a2 + b2 + c1 = 1 + 0 + 1 = 1 × 2 + 0,
    so that c2 = 1 and s2 = 0. Finally, because a3 + b3 + c2 = 1 + 1 + 1 = 1 × 2 + 1,
    follows that c3 = 1 and s3 = 1. This means that s4 = c3 = 1. Therefore, s = a + b = (11001)2.
  2. MULTIPLICATION ALGORITHM: Consider the multiplication of two n-bit integers a and b. The conventional algorithm (used when multiplying with pencil and paper) works as follows. Using the distributive law, we see that
    ab = a(b020 + b121 + ‧ ‧ ‧ + bn − 12n − 1)
    : = a(b020) + a(b121) + ‧ ‧ ‧ + a(bn − 12n − 1)
Primes and Greatest Common Divisors
Primes

A prime is an integer that is divisible by two positive integers, 1 and itself.

Prime numbers are quite important as they are used in modern cryptographic systems. The length of time required to factor large integers into their prime factors is the basis for the strength of these systems.

Definition 1: An integer p greater than 1 is called prime if the only positive factors of p are 1 and p. A positive integer that is greater than 1 and is not prime is called composite.

Definition 2: If n is a composite integer, then n has a prime divisor less than or equal to √ n .

The Sieve of Eratosthenes
  1. The sieve of Eratosthenes is used to find all primes not exceeding a specified positive integer. For instance, the following procedure is used to find the primes not exceeding 100.
  2. Because the only primes less than 10 are 2, 3, 5, and 7, the primes not exceeding 100 are these four primes and those positive integers greater than 1 and not exceeding 100 that are divisible by none of 2, 3, 5, or 7.
Conjectures and Open Problems About Primes

There are few conjectures which have not yet been proved. Below are few conjectures whose proofs has not been found

  1. Goldbach's ConjectureAny even number greater than 2, can be written as sum of two primes.
  2. The twin prime conjecture asserts that there are infinitely many twin primes
  3. There are infinitely many primes of the form n2 + 1, where n is a positive integer.
Greatest Common Divisors and Least Common Multiples

Greatest common divisor (gcd) The largest integer that divides both of two integers.

The Euclidean Algorithm

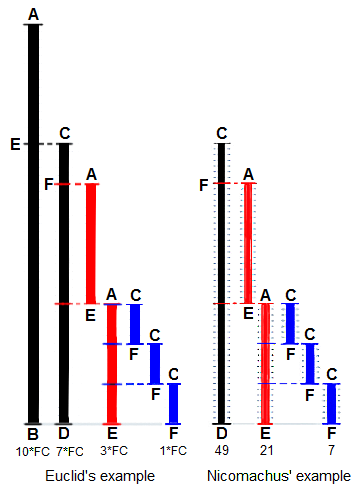
Euclidean Algorithm
Computing gcd using prime factorization is a time consuming process. The Euclidean algorithm gives an `efficient way to compute gcd.
Steps To find gcd(a, b)

  1. Divide the larger of two numbers (say a) by the smaller number (say b), let the remainder be (c).
  2. Now, the problem changes to finding gcd(b, c)
  3. Continue the above procedure, till one of the integers is 0.
gcd as a Linear Combination
More definitions
  1. Relatively prime Two numbers are said to be relatively prime if their gcd is 1.
  2. Least Common Multiple (lcm) the smallest integer that is divisible by both a and b.
    If a and b are positvie integers then, a × b = gcd(a, b) × lcm(a, b)
Solving Congruences

Linear Congruences A congruence of the form ax ≡ b (mod m), where m is a positive integer, a and b are integers, and x is a variable, is called a linear congruence.

We need to find the values of x which will solve the congruence. The theorem below, gives one such method to solve congruences.

Theorem 1 If a and m are relatively prime integers and m ≥ 1, then an inverse of a modulo m exists which is unique. And every inverse of a modulo m is congruent to a modulo m.

The Chinese Remainder Theorem

Let m1,m2, ... , mn be pairwise relatively prime positive integers greater than 1 and a1, a2, ... , an be arbitrary integers. Then, x ≡ a1 (mod m1), x ≡ a2 (mod m2), x ≡ an (mod mn) has a unique solution modulo m &euiv; m1m2 ∗ ∗ ∗mn. (That is, there is a solution x with 0 ≤ x < m, and all other solutions are congruent modulo m to this solution.)

Fermat's Little Theorem

If p is prime and a is an integer not divisible by p, then ap − 1 ≡ 1 (mod p). Furthermore, for every integer a we have ap ≡ a (mod p).

Definitions
  1. Pseudoprime
    If n is a composite number and b is a positive integer, then, if b n-1 ≡ 1 (mod n), then n is a pseudoprime, with respect to b
  2. Carmichael number A composite number n which satisfies the congruence b n− 1 ≡ 1 (mod n) for all positive integers b and gcd(b, n) = 1
  3. Primitive root A primitive root modulo of a prime p is an integer r, such that every power of r is an element of Z p
  4. Discrete Logarithm Suppose that p is a prime, r is a primitive root modulo p, and a is an integer between 1 and p − 1 inclusive. If r e mod p = a and 0 ≤ e ≤ p − 1, we say that e is the discrete logarithm of a modulo p to the base r and we write log r a = e.
Applications of Congruences

Congruences are applied in many fields of computer Science, like assigning memory address to file systems, generating pseudorandom numbers, check digits etc.

Hashing Functions

Records in database are stored and identified using unique id. These id's are stored at a location formed using hashing functions.

A hashing function assigns memory address h(k) to a record that has key k.One of the most common used for this is h(k) = k (mod m)

To find h(k), we need only compute the remainder when k is divided by m. Furthermore, the hashing function should be onto, so that all memory locations are possible

Pseudorandom Number

Linear congruential method is generaly used for generating pseudorandom numbers.We need four integers

  1. modulus m
  2. multiplier a, with 2 ≤ a < m
  3. increment c, with 0 ≤ c < m
  4. seed x0 with 0 ≤ x0 < m.

a pseudorandom number {xn} is recursively generated such that 0 ≤ xn < m for all n xn+1 = (a xn + c) mod m

Check Digits

These are used to verify correctness of a particular string, and finds its application in digital information, verifying product codes etc.

An extra digit is added at the end of string. This final digit is then checked to see whether the value is correct or not

  1. Parity check bits
  2. Universal code products
  3. International standard book number
Cryptography
Introduction

Cryptography is a way of concealing messages from everyone except from reciever and sender and is also used for authentication

Classical Cryptography

In classical cryptography, the letters were replaced by one less than the position of alphabet (for example: A is replaced by 0, Z by 25) and then adding 3 to the number, which is equivalent to shifting the letter by 3

Public Key Cryptography

Private key cryptography requires the key which is used to encrypt the message to be shared between the recieveing and sending parties. Hence, public key cryptosystems where introduced. In this knowing how to send an encrypted message does not help decrypt messages.

The RSA Cryptosystem

In the RSA cryptosystem, each individual has an encryption key (n, e) where n = pq, the modulus is the product of two large primes p and q, and an exponent e that is relatively prime to (p − 1) (q − 1).To produce a usable key, two large primes must be found.

RSA Encryption

A plaintext message M is converted into a sequence of integers m1, m2, . . . , mk for some integer k. Encryption proceeds by transforming each block mi to a ciphertext block ci . This is done using the function C = Me mod n.

RSA Decryption

The plaintext message can be quickly recovered from a ciphertext message when the decryption key d, an inverse of e modulo (p − 1)(q − 1), is known. An inverse surely exists because gcd(e, (p − 1)(q − 1)) = 1

RSA as a Public Key System

RSA is used as public key system as it is easily possible to construct a public key by finding two large primes p and q, and to find an integer e relatively prime to (p − 1) (q − 1). When we know p and q, we can easily compute the inverse d of e modulo (p − 1) (q − 1).

Factorization is difficult as opposed to finding large primes p and q. The most efficient factorization methods known require billions of years to factor 400-digit integers.

Cryptographic Protocols

Cryptographic protocol is exchange of messages between two parties over an insecure communication channel. This requires forming a key to be shared between both parties.

the following protocol is followed:

  1. A prime number say p and a primitive root of p, say a is agreed to be used by both parties.
  2. The first party chooses a secret integer k1 and sends ak1 mod p to the second party
  3. The second party chooses a secret integer k2 and sends ak2 mod p
  4. Alice computes (ak2)k1 mod p. Second party computes (ak1)k2 mod p which is the shared key

The protocol ensures that k1, k2, and the common key are kept secret,no other method is known for finding the shared key using just the public information.