Relations

Powerset of three.
Introduction

In Mathematics, A relation between elements of two sets can occur in many contexts. Like consider a relation between two sets of stations linked through trains.

A relation set between two relations say A and B is a subset of cartesian products of A and B

Relations and Their Properties
Introduction

Ordered Pairs can be used to express relation between two elements. These are called as binary relations.

DEFINITION 1:

A binary relation from A to B is a subset of A x B;

Example Let A = {0,1,2} and B = {1,2} then a relation set of {x | x ∈ R x =x} is given by {1,1} ,{2,2}

Functions as Relations

A relation between a function from A to B is defined by assigning exactly one element of B to A;

The graph of f is the set of ordered pairs (a, b) such that b = f (a).

Example A relation on a set A is a subset of A x A. Because A x A has n2 elements

when A has n elements, and there are 2 n2 subsets of A x A. Thus, there are 2 n2 relations on a set with n elements.

Relations on a Set
DEFINITION 2:

A relation on a set A is a relation from A to A.

Properties of Relations
DEFINITION 3:

A relation R on a set A is called reflexive if ((a, a) ∈ R) for every element a ∈ A.

DEFINITION 4:

A relation R on a set A is called symmetric if (b, a) ∈ R whenever (a, b) ∈ R , for all

a, b ∈ A. A relation R on a set A such that for all a, b ∈ A, if (a, b) ∈ R and (b, a) ∈ R, then a = b is called antisymmetric.

DEFINITION 5:

A relation R on a set A is called transitive if whenever (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R, for all a , b , c ∈ A.

DEFINITION 6:

Let R be a relation from a set A to a set B and S a relation from B to a set C. The composite of R and S

is the relation consisting of ordered pairs (a, c), where a ∈ A, c ∈ C, and for which there exists an element b ∈ B

such that (a, b) ∈ R and (b, c) ∈ S. We denote the composite of R and S by S ◦R.

Representing Relations
Introduction

Relations can also be expresed using zero-one matrices and directed graphs. We are considering relations to be binary relations hereon.

Representing Relations Using Matrices

using zero-one matrices.If two sets A and B are equal then the relation R between them is given by:

mij = 1 if (ai , bj) ∈ R and mij = 0 if (ai , bj) ∉ R

Example:

Representing Relations Using Digraphs

Relations can be expressed using Directed graphs (Digraphs), in this elements of sets are represented by a point,

and all the ordered pairs are represented using an edge with their direction shown using arrows.

DEFINITION 1:

A directed graph, consists of a set vertices and a set of ordered pairs of elements of vertices called edges.

The vertex from which the arc starts is called the initial vertex , and the vertex where the arc terminates is called the terminal vertex.

a is initial and b is terminal vertex.

Example Draw a directed graph of the following ordered pairs: {(1, 1), (1, 3), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (4, 1)}

Closures of Relations
Introduction

Let R be relation containing ordered pairs (a, b)

which determine connection between two cities. If there is no direct connection between two cities,

then the ordered pair won't exist in the Relation set, even though there is a connection indirectly.

In such cases, we need to construct a transitive relation S which is a subset of R such that it contains all the transitive relations in R

This is called as transitive closure

Closures

Reflexive closure: A relation that contains reflexive pairs, for example, a relation set R of an ordered pair of (a, b) should contain (a, a ) and (b , b) ∈ R to form a reflexive closure

Paths in directed graphs

Definition 1: A path in a directed graph form (a ,b) is sequence of vertex from a to b where terminal vertex of an edge is the same as the initial vertex in the next edge in the path.

Theorem: Let R be a relation on a set A. There is a path of length n, where n is a positive integer, from a to b if and only if (a, b) ∈ R n.

Equivalence Relations
Equivalence Relations

Definition 1: A relation is called an equivalence relation if it is reflex, transitive and symmetric

Definition 2:Two elements that are related by an equivalence relation are called equivalent. ~ is used to denote that two elements are equivalent elements with respect to a particular equivalence relation.

Example Is multiply relation in the set of positive integers an equivalence relation ?
Equivalence class
Definition: It is a class of all members of a set that are given in an equivalence relation. If R is an equivalence relation on a set,then the set of all elements that are related to an element of Set is called the equivalence class of that element of Set.
Congruence is an example of an equivalence relation. The leftmost two triangles are congruent, while the third and fourth triangles are not congruent to any other triangle shown here. Thus, the first two triangles are in the same equivalence class, while the third and fourth triangles are each in their own equivalence class.
Equivalence Classes and Partitions
Introduction

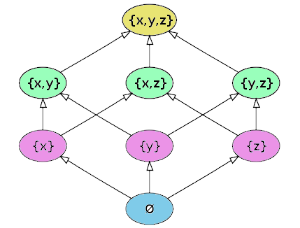
Equivalence class of an equivalance relation partitions a set into disjoint, nonempty subsets.

Theorem 1: If R is an equivalence relation on set A, then
  1. aRb
  2. [a]=[b]
  3. [a] ∩ [b] ≠0
for elments a and b in set
Partial Orderings
Introduction

A set with a binary relation R such that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering that is partial order is created

Definition 1: A relation on a set is called partially ordered, if it is reflexive, symmetric and transitive. The set along with R is called poset
Example: Show that a ≥ b forms a poset
Definition 2: Elements of a poset (S, ≤) are said to be comparable, if the elements say a , b in S hold the relation a ≤ b or b ≤ a
Definition 3: If in a poset (S, ≤) every two elements of S are comparable, then S is called a totally ordered or linearly ordered set or a chain.
Definition 4: (S, ≤) is a well-ordered set if it is a poset such that ≤ is a total ordering and every nonempty subset of S has a least element.

least element is an element of S that is smaller than every other element of S

Example: The set Z, with the usual ≤ ordering, is not well-ordered because the set of negative integers, which is a subset of Z, has no least element.

Theorem 1: THE PRINCIPLE OF WELL-ORDERED INDUCTION: Suppose that S is a wellordered set. Then P(x) is true for all x ∈ S, if For every y ∈ S, if P(x) is true for all x ∈ S with x ≤ y , then P(y) is true.
Lexicographic Order

This is the ordering which is based on ordering of letters in alphabet. The words in a dictionary are arranged in lexographic order

The lexographic order on two posets (A , ≤) and (B, ≤) is defined by specifiying that one pair is (a0, b0) is less than (a 1, b1), that is, (a1, b1) ≤ (a2, b2),either if a ≤ b or if both (a1 = b1) and a2 ≤ b2.

Hasse Diagram

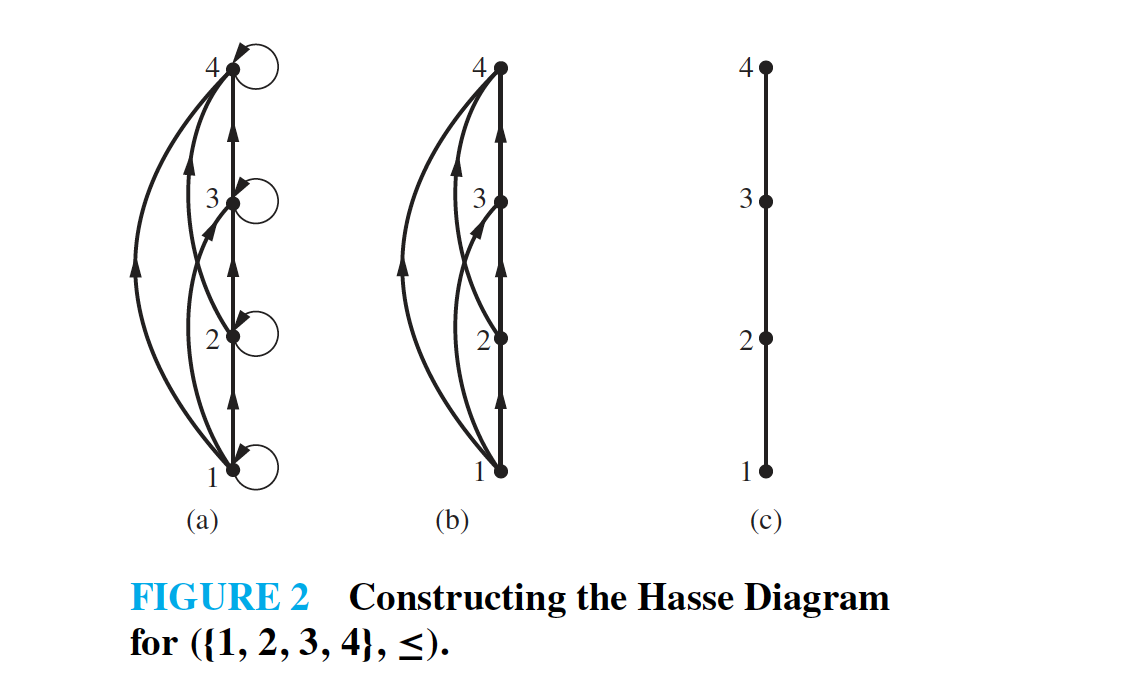
As we know from above discussions that Partial Ordering is reflexive, transitive. Hence in a directed graph for a poset, say {(a, b) | a ≤ b} on the set {1, 2, 3, 4} we don't have to show loops for all the vertices ( 1, 2, 3 and 4), as it is implicit.

Similarly, as the poset hold transitivity, if (1 < 2) and (2 < 3) this implies that (1 < 3) hence, we don't need to show a directed edge from 1 to 3.

If we assume that all edges are pointed upwards, we need not show the direction of vertices

Hasse diagram, partial ordering. Image source:Rosen_Dicrete_Mathematics_and_it's_application
Maximal and Minimal Lattice

An element in a poset is called maximal if there is no element in set greater than that element.

Similarly, an element is called minimal if there is no element lesser than that in a set

Hasse diagram can be easily used to find maximal and minimal elements as they are respectively top and bottom elements in the diagram

Definitions
      least element

    An element which is lesser than all other elements in the set.It is unique when it exist

      greatest element

    An element greater than every element in the set and is unique when it exist

      upper bound

    An element which is greater than or equal to all the elements in the subset is an upper bound

      lower bound

    An element which is less than or equal to all the elements in the subset is a lower bound

      least upper bound

    An element x is called a least upper bound of a set A if it is lesser than all other upper bounds of A there is only one such element like this

      greatest lower bound

    An element which is greater than all the lower bounds of a set is a greatest lower bound. There is only one such element

Lattices

A poset in which every pair of elements has both a least upper bound and a greatest lower bound is called a lattice.

Topological Sorting
Introduction

The cases where certain task can be completed only after some other task are completed, partial ordering can be done. Topological sorting can be used to construct total ordering from partial ordering

LEMMA 1: Every finite nonempty poset (S, ≤) has at least one minimal element.

Credits