Design and Analysis of Algorithms: Divide and Conquer

Introduction

What is this?

Introduction to divide-and-conquer
Recurrences

Merge sort recurrence:



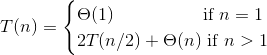
We "solve" these by finding a closed-form equation that describes the recurrence but without recursion.
Solution: T(n) = Θ(n lg n)

Methods:


Technicalities
We often omit floors, ceilings, and boundary conditions. For instance, if n is odd, we may say n / 2 anyway.

4.1 The maximum-subarray problem



Only makes since in an array with both negative and positive values: otherwise the answer is either the whole array or the maximum member.

Brute-force solution

Try every combination of two elements!
A n choose 2 problem, so order of Ω(n2).
n choose 2 will be about 1/2 n2, since it equals n(n - 1) / 2. So we can establish a lower bound by setting c = 1/3, for instance, and n choose 2 will always be bounded from below by c*n2.

A transformation

We look at the problem differently: let's find the nonempty, contiguous subarray of our array whose values have the largest sum. We call this the maximum subarray.

A solution using divide-and-conquer

To solve this problem, we divide an array A into three subarrays, and ask what is the maximum subarray in each:

  1. From A[low] to A[midpoint - 1].
  2. Crossing the mid-point.
  3. From A[midpoint + 1] to A[high]

Problems 1 and 3 are simply this same problem on a smaller array! Problem 2 can be solved by finding the maximum subarrays in low-to-mid and in mid+1-to-high.

The recurrence is the same as for merge sort.

Run the Python code

In the console below, type or paste:
!git clone https://gist.github.com/25ffc0600a866535adef05c5d8eca34a.git
cd 25ffc0600a866535adef05c5d8eca34a
from find_max_subarray import *
A = [13, -3, -25, 20, -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7]

Python console

To run the example from the textbook, type:
A
find_max_subarray(A, 0, 15)

Now you can experiment with the algorithm by typing in your own array (my_array = [x, y, z]) and running find_max_array(my_array).

Video on maximum subarray problem
Maximum sub-array video
Quiz
  1. The problem with the brute force max-subarray solution is
    1. it is too complicated
    2. the force used might break the code
    3. it is too slow
  2. The three possible arrays containing the maximum sequence are
    1. An array of ints, an array of doubles, and an array of strings
    2. The array from A[0] to the mid-point; an array that crosses the midpoint, and the array from A[midpoint + 1] to the end
    3. The whole array, the null array, and the middle array
  3. What does FIND-MAXIMUM-SUBARRAY return when all elements of A are negative?
    1. Largest Positive Number in A
    2. Largest Negative Number in A
    3. First index of A
    4. Lase index of A
Answers

1. c; 2. b; 3. b;

4.2 Strassen's algorithm for matrix multiplication
Recursive Square-Matrix Multiply

We divide each of our initial matrices into four sub-matrices, and multiply them. Which we do by dividing each of them into four...

In the base case when each matrix has only one member, we just multiply them and return the result.

So what is our recurrence? Each step except the base case multiplies eight matrices of size n / 2. So they contribute 8T(n / 2) to running time. There are also four matrix additions of matrices containing n2 / 4 entries -- squared because n specifies an n x n matrix. So this contributes Θ(n2) time.

So our recurrence is:



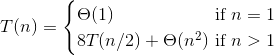
The master method will show us that the solution to this recurrence is:
T(n) = Θ(n3)

Run the Python code

In the console below, type or paste:
!git clone https://gist.github.com/87e1f86c634c1538062041ca153bc466.git
cd 87e1f86c634c1538062041ca153bc466
from divide_conquer_matrix import *
A = [[1, 3], [7, 5]]
B = [[6, 8], [4, 2]]

Python console

To run the example from the textbook, type:
A,B
square_matrix_multiply(A, B)
square_matrix_multiply_recursive(A, B)

Now you can experiment with the algorithm by typing in your own Matrix (my_matrix = [x, y, z]) and running square_matrix_multiply(a_matrix, b_matrix) or square_matrix_multiply_recursive(a_matrix, b_matrix).

Strassen's Algorithm



By adding ten additions, we can cut the divide portion of our algorithm down to seven multiplications instead of eight.

Let's try one!

Here is the method:

For two matrices:



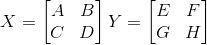
Define:

P1 = A(F - H)
P2 = H(A + B)
P3 = E(C + D)
P4 = D(G - E)
P5 = (A + D) * (E + H)
P6 = (B - D) * (G + H)
P7 = (A - C) * (E + F)

Then:



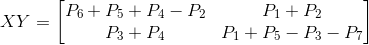
So let's try this example:



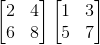
Important Lesson

There are often serious trade-offs between set-up time and aymptotic run-time. One must carefully consider how large one's inputs are likely to be before opting for a complex algorithm like Strassen's. On modern hardware optimized for matrix multiplication, matrix sizes often need to be in the thousands before Strassen's algorithm yields significant gains.

4.3 The substitution method for solving recurrences

Note: I am presenting these three methods in my notes in textbook order. But in lectures, I present the substitution method last, because we can best make sense of our "guess" for a solution if we understand the other two methods first. I suggest students tackle recursion-tree, then master method, and then substitution.

Towers of Hanoi

Shared web material located here.

Another substitution-method problem

Let's look at the recurrence:
T(n) = T(n/3) + T(2n/3) + n
T(0) = 1
T(1) = 1

This does not have the form the master method requires. And if we sketch a recursion tree, not every node is the same on a level, so it is different from what we usually deal with there. But if we do diagram a recursion tree, we will see that the work looks constant at each level, like a master theorem case 2. And since the function part of the equation is f(n) = n, let's "guess":
T(n) ≤ cn log n

But that is just our hunch: we have to prove it!

Let's look at base cases for our inductive proof. Use floors for divisions! Is:

How many base cases do we need to examine? We will see!
But we can prove it for any given "small" n > 2 by setting:
c ≥ T(n) / n log n

Recursion step:
We assume that for k where:
2 ≤ k < n
the claim is true.
Now, we need to show that if for sub-problems smaller than n the claim is true, then it is true for n.

4.4 The recursion-tree method for solving recurrences

There are two ways to use this method:

  1. As a way to generate a guess for the substitution method.
  2. As a way to generate a rigorous answer by itself.

Analyze the tree:



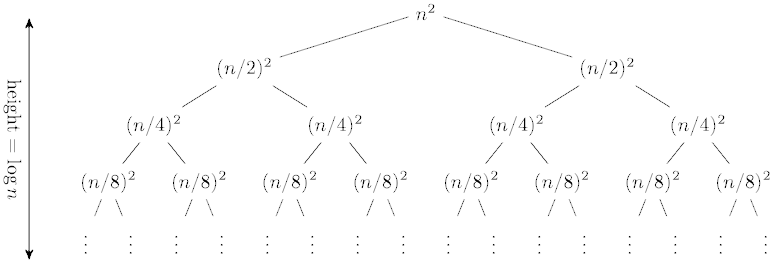
Calculate the work at each level:



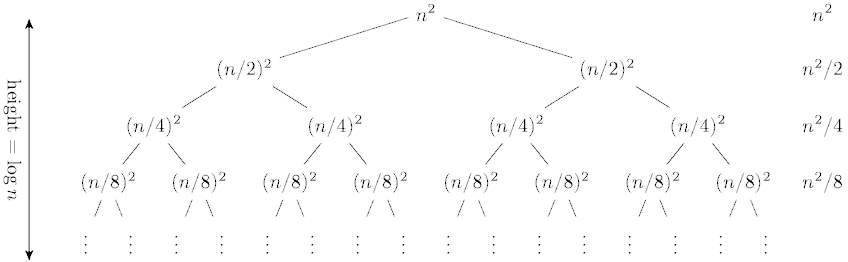
This produces the geometric series:



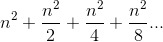
If we set a = n2 and r = 1/2, then we have the general sum of a converging geometric series:



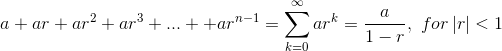
So the solution here is O(n2). The amount of work at each level is reduced by a power of two, and so is just a constant factor times the root.

Consider these three examples:

  1. T(n) = 4T(n/2) + cn
  2. T(n) = 2T(n/2) + cn
  3. T(n) = 2T(n/2) + cn2
    (This is the recurrence in the diagram above.)

(We assume c > 0.)
Let's break down these cases:

T(n) = 4T(n/2) + cn1
Level # Nodes Work at
Node 		Work at
Level
0 1 n n
1 4 n/2 2n
2 16 n/4 4n
3 64 n/8 8n
i 4i n/2i 2in
h =
log2n 		4h T(1) 4hT(1)

The runtime then is:

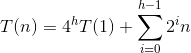
h = log2n
so the first part equals:
4log2n = nlog24
We pull out the n from the sum and it is an increasing geometric series that evaluates to n − 1. So the closed form for the recurrence is:
n2T(1) + n(n - 1)

The very last level dominates, as it already has O(n2) complexity.

T(n) = 2T(n/2) + cn1
Level # Nodes Equ. for
Node 		Work
0 1 n cn
1 2 n/2 cn
2 4 n/4 cn
3 8 n/8 cn
i 2i n/2i cn
h =
log2 n 		2h T(1) 2hT(1)

And so we get:

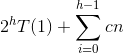
2h = n.
The sum happens log n times, so we have cn * log n.

All levels contribute equally.

T(n) = 2T(n/2) + cn2
Level # Nodes Equ. for
Node 		Work
0 1 n2 n2
1 2 (n/2)2 n2/2
2 4 (n/4)2 n2/4
3 8 (n/8)2 n2/8
i 2i (n/2i)2 n2/2i
h =
log2n 		2h T(1) 2hT(1)

The runtime then is:

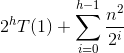
We pull out the n2 from the sum, and we get a geometric series. Obviously, n2 dominates. And it is the same as the top level.

These all have the form: T(n) = aT(n / b) + f(n).
When we work these out, we see that in our 3 cases:

  1. The recursion is the dominant factor, and the bottom level has the Big-O complexity of the whole recurrence.
  2. The recursion and f(n) contribute equally to the run time, and all levels are equal.
  3. f(n) dominates, and the top level has the Big-O complexity of the whole recurrence.

This observation leads us to:

4.5 The master method for solving recurrences

Form: T(n) = aT(n / b) + f(n).
Where a ≥ 1 and b > 1 and f(n) asymptotically positive.

Three cases
Compare nlogba and f(n):

  1. f(n) = O(nlogba-ε), ε > 0
    Solution: T(n) = Θ(nlogba)
  2. f(n) = Θ(nlogba)
    Solution: T(n) = Θ(nlogba lg n)
  3. f(n) = Ω(nlogba+ε), ε > 0
    Solution: T(n) = Θ(f(n))

Restrictions:

  1. a ≥ 1
    We must divide the problem into at least one sub-problem.
    The method will work if a is not an integer, although this doesn't really make sense: how can we have 1.5 sub-problems?
  2. b > 1
    If we don't get smaller sub-problems, we will never finish! (n/b < n)
  3. Regularity condition for case 3: af(n/b) ≤ cf(n)

    Notice the gap between the red and blue lines:
    The "polynomial line"


    The master theorem will not apply in that gap!

    Consider:
    T(n) = 2T(n/2) + n log n
    n log n grows faster than n, but not by a polynomial difference:
    log n is asymptotically < nε for any ε > 0
    A spreadsheet where you can see this for yourself.


    Detailed Example:
    The master theorem won't apply in this case:
    T(n) = 4T(n/2) + (n2/log n)

    The first part gets us n2.
    (n2/log n) = O(n2)

    (n2/log n) / n2 = 1 / log n
    which goes to 0 as n goes to infinity.

    But is it polynomially larger than (n2/log n), so that we are in case 1? Or, is there an ε we can subtract from 2 so that n2-ε is still an upper bound for (n2/log n)?
    Is f(n) = O(nlogba-ε) ?

    Let's look at the ratio:
    (n2/log n) / n2-ε

    That yields:
    nε / log n → ∞ as n → ∞.
Quiz
  1. Using master method (mm), the runtime for T(n) = 3T(n/2) + n2 is:
    1. n log n
    2. Θ(n3/2)
    3. MM does not apply
    4. Θ(n2)
  2. Using mm, the runtime for T(n) = 2n(n/2) + nn is:
    1. Θ(n)
    2. MM does not apply
    3. Θ(2n)
    4. Θ(nn)
  3. Using mm, the runtime for T(n) = 0.5T(n/2) + 1/n is:
    1. Θ(.5n)
    2. Θ(n)
    3. MM does not apply
    4. Θ(1/n)
Answers

1. d; 2. b; 3. c;

Source Code

Java
Ruby
Python

For Further Study
Homework

On NYU Classes.

Credits