Design and Analysis of Algorithms: Growth of Functions

A review of Big-O, summations and algebra.
Different asymptotic notations
Big O
Notation Intuition Definition
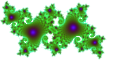
g(n) = O(f(n)) g is bounded above by f (up to constant factor) asymptotically g(n) ≤ k*f(n) for some positive k, after some n
Big Θ
Notation Intuition Definition
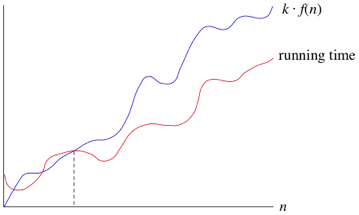
g(n) = Θ(f(n)) g is bounded above and below by f asymptotically k2*f(n) ≤ g(n) ≤ k2*f(n) for some positive k1, k2
Big Ω
Notation Intuition Definition
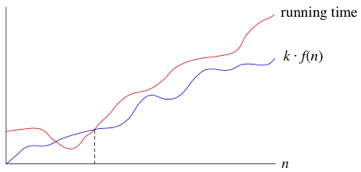
g(n) = Ω(f(n)) g is bounded below by f asymptotically g(n) ≥ k*f(n) for some positive k
Little o
Notation Intuition Definition
g(n) = o(f(n)) g is dominated by f asymptotically g(n) < k*f(n) for every positive k
Little ω
Notation Intuition Definition
g(n) = ω(f(n)) g dominates f asymptotically g(n) > k*f(n) for every positive k
Why have different notations?

Why not just Big-Θ?

From the Khan Academy site:

We use big-Θ notation to asymptotically bound the growth of a running time to within constant factors above and below. Sometimes we want to bound from only above. For example, although the worst-case running time of binary search is Θ(lg n), it would be incorrect to say that binary search runs in Θ(lg n) time in all cases. What if we find the target value upon the first guess? Then it runs in Θ(1) time. The running time of binary search is never worse than Θ(lg n), but it's sometimes better. It would be convenient to have a form of asymptotic notation that means "the running time grows at most this much, but it could grow more slowly." We use "big-O" notation for just such occasions.

Highest-order term

Graphs and a table on why we only care about the highest-order



n Fast Alpha machine,
C code,
running O(n3) algo. 		TRS-80
interpreted Basic,
running O(n) algo.
10 .6 microsecs. 200 millisecs.
100 .6 millisecs. 2 secs.
1000 .6 secs. 20 secs.
10,000 10 mins. 3.2 mins.
100,000 7 days 32 mins.
1,000,000 19 years 5.4 hours

(Table from Jon Bentley, Programming Pearls.)

Notes on log functions.

The textbook uses lg for base-2 logarithms. But... the base doesn't really matter! Why?

n log base-2 log base-10 Differ by...
2 1 .301 3.322
10 3.322 1 3.322
32 5 1.505 3.322

They differ by a constant factor!
Log rule: logb(x) = logc(x) / logc(b)
So... log10(32) = log2(32) / log2(10)
= 5 / 3.322 = 1.505

Also, let's look at logs versus polynomial growth. Even for very small powers p > 0, xp grows faster than log x. Below we use natural logs:

p xp > log x at
.3 379
.2 332,105
.1 3,430,631,121,407,801
Meaning of constants in O, Θ and Ω expressions

Let's say we posit a search operating in 2n + 3 time.
We want to show that this has Θ(n) complexity.
We must find k1, k2, and n0, so that: k1 * n < 2n + 3 < k2 * n
One solution is k1 = 1, k2 = 3, and n0 = 4.

Algorithmic design in action
Fibonacci numbers

The problem of computing, given n ≥ 0, the nth Fibonacci number Fn.

The Fibonacci discussion is not in the textbook. One place where it is presented in a nice way similar to what I will do in class is in section 0.2 of the DasGupta, Papadimitriou, Vazirani Algorithms book.

Talked about the obvious recursive algorithm; how it is very slow, intuitively due to recomputing the same subproblems. Proved that the recursion tree grows at least as fast as the Fibonacci sequence itself.

Sketch of Proof

Note that every leaf of the recursion tree returns one. The sum of the value of all of these leaves is going to be the Fibonacci number we return. Therefore, there must be at least as many operations as the Fibonacci number itself.

Showed how to speed the recursive algorithm algorithm up by "memoization": Using a table to store answers for subproblems already computed. Analyzed the running time and space of the recursive memoized version and of the iterative algorithm that fills the table going in the forward direction. Pointed out how to reduce space to constant.

Naive and faster Fibonacci code.

By the way, this is an open-source project: you may contribute!

There is a closed-form formula for computing Fibonacci numbers.

So why can't we claim we can compute nth Fibonacci number in constant time? Did not go into details, but this is related to our inability to directly represent irrational numbers such as square roots, maybe related to precision/rounding, and generally related to what operations are allowed and what are not, in an algorithm.

Using some tricks one can construct nth Fibonacci number in O(log n) arithmetic operations, where we count additions/subtractions/multiplications and do not worry about the fact that eventually the numbers get too large to manipulate in constant time.

Data structures

Data structures form a very important part of algorithmic research.

However, this course does not focus on data structures. We will only devote a couple of lectures, total, to this subject. (There are algorithms courses that spend their entire time on data structures. We have an advanced data structures expert in the department, Prof. John Iacono.)

Detailed case study: Iterables as an ADT.
Basic operations.
  • Get iterator.
  • Get next value.
  • Detect end of iterables.
Extended operations.
  • Rewind? We may not be able to if the iterator is exhausted in iterating through it.
  • Iterate in reverse?
  • Access an arbitrary element? (By index, say.)
Implementations.
  • Straight-forward: Array.
  • More complex: Python lists: somewhat like an array, but also like a linked list.
Homework
  1. if f(n) = 3n2 + n3 lg n, then f(n) is
    1. O(n2)
    2. O(n3/2)
    3. O(n3 lg n)
    4. O(n2/3)
  2. What is the asymptotic relationship between the functions: xp and kx? (Assuming that p ≥ 1 and k > 1 are constants:)
    1. xp is O(kx)
    2. kx is O(xp)
    3. x is O(k)
    4. Both b and c
  3. For functions, nk and cn , what is the asymptotic relationship between these functions? Assume that k ≥ 1,and c ≥ 1 are constant.
    1. nk is O(cn)
    2. nk is Ω(cn)
    3. nk is Θ(cn)
    4. None of the above
  4. If f(n) = 5 lg n + 2 lg n! + (n2 + 1) lg n, what is the big-O notation for f(n)?
    1. n
    2. n2
    3. n lg n
    4. n2 lg n
  5. What is the time complexity for the following piece of code? 
                    
                 sum = 0;
                 for (int i = 0; i < n; i++)
                     for (j = 1; j < n; j = j * 2)
                         sum += n;
    1. O(n2)
    2. O(n)
    3. O(lg n)
    4. O(n lg n)
  6. If f(x) = (x3 − 1) / (5x + 1) then f(x) is
    1. O(x2)
    2. O(x)
    3. O(x3/5)
    4. O(1)
  7. The Big-O complexity of 1 + 2 + 3 + 4 ... + n is? (Assume we must add the numbers one at a time, rather than using Gauss's trick to get a closed form for the sum.)
    1. O(n)
    2. O(n2)
    3. O(3n)
    4. O(n3)
  8. The Big-O complexity of 1 + 2 + 3 + 4 + ... + 100 is? (Assume we must add the numbers one at a time, rather than using Gauss's trick to get a closed form for the sum.)
    1. O(1)
    2. O(n)
    3. O(n2)
    4. O(3n)
  9. What is big O for following code? 
                    
                    void complex(int n)
                    {
                        int i, j;
                        for(i = 1; i < n; i++) {
                            for(j = 1; j < log(i); j++)
                        }
                        printf("Algorithms");
                    }
  10. What is big O for following code? 
                    
                    void complex(int n)
                    {
                        int i;
                        for(i = n; i > 1; i = i/2){
                            printf("Algorithms")
                        }
                    }
* Based on Prof. Boris Aronov's lecture notes.
** Material drawn from Khan Academy.