Design and Analysis of Algorithms: Hash Tables *

Operations associated with this data type allow:

• the addition of a pair to the collection
• the removal of a pair from the collection
• the modification of an existing pair
• the lookup of a value associated with a particular key

(Source)

Typical uses:

• Symbol lookup in a programming language
• Counting words in a book
• Store colors by name as key and their numeric equivalent as the value. Then we can write set_text(colors["red"]).

Direct addressing and Hashing are two ways of implementing a dictionary. Are there others?

                    Direct-Address-Search(T, k)
                        return T[k]

                    Direct-Address-Insert(T, x)
                        T[x.key] = x

                    Direct-Address-Delete(T, x)
                        T[x.key] = NIL
                    

1. A good use for a direct-address table might be:
1. All answers are fine
2. Memoization
3. Bingo
4. Marking members of a set as present
2. We can't use direct-address tables when
1. there are a large number of (potential) entries
2. all answers are fine
3. we are programming the Sieve of Eratosthenes
4. we are dealing with zipcodes
3. What is direct addressing?
1. Fewer keys than array positions
2. Every key specifies a distinct array position
3. Fewer array positions than keys
4. None of the mentioned

• O(1) average case time for lookup.
• Universe of keys U mapped into slots of a hash table of size m by hash function h.
• Because size(U) > m, collisions are always possible.
  Imagine we hash by word length: 'mark' and 'beam' both hash to 4. (Stupid hash function, but it illustrates the idea.) We must resolve this collision somehow.
• Resolve collisions by chaining:
  Each slot holds a linked list of values.
• Cryptographic hashing
  Use large hash keys: SHA-1 uses 160 bit keys. SHA-2 uses keys of up to 512 bits.
  
• Perceptual hashing

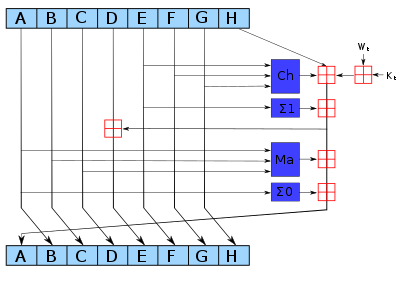
What happens to the usual assumptions?
Correctness: always, most of the time?
Termination: always, or almost always? What does "performance" mean if the running time/answer/even termination change from one run to the next?

Reviewed in this document.

This employs chaining. Furthermore, we assume that the distribution of elements is uniform across hash table slots.

• Hash table T with m slots storing n elements.
• Load factor: α = n / m
  α is the average number of elements stored in a chain.
• Our analysis is in terms of α, which can be less than, equal to, or greater than one.
• Worst case is very bad:
  All n keys hash to the same slot.
  Worst case for searching becomes Θ(n) plus time to compute hash function.
  We could have just used a linked list directly!
• Average case:
  Assuming any given element is equally likely to hash into any slot...
  We get average case Θ(1 + α) time.
  Unsuccessful search: the average chain length will be α. Thus, after finding the right slot with a hash function that runs in O(1) time, we will search α expected elements before giving up, giving us he above run time.
  Successful search: The probability that a list will be searched is proportional to the number of items it contains. Nevertheless, we still expect α items to be searched.
• This means that if our table size is roughly proportional to n, then we have n = O(m), and α = n / m, and so α = O(m) / m, and so α = O(1). And thus the whole search is O(1).

Consider the following hashing scheme:
h(k) = k mod m
m = 7
We convert a string into a hashable key by treating it as a base-8 number.
So 'abc', where a = 1, b = 2, and c = 3, is converted to a key as follows: 1 * 8² + 2 * 8 + 3 = 83.
In this hashing scheme, what do the strings 'cba' and 'bac' hash to?
Can you write a more general statement about a pattern we can detect here? Something along the lines of, "If the table size is 2^P - 1, and strings are interpreted in radix 2^P..."

Answer:
If h(k) = k mod m, where m = 2^P − 1, and k is a character string interpreted in radix 2^P, then all permutations of a given string will hash to the same value. So in the example above, 'abc', 'cba', and 'bac' all hash to the same value.

Proof:
Assumed (could be proven, but we won't do it here):

1. (x + y) mod z == (x mod z + y mod z) mod z
   Example: (10 + 12) mod 7 == (10 mod 7 + 12 mod 7) mod 7
2. (x * y) mod z == (x mod z) * (y mod z) mod z
   Example: (10 * 12) mod 7 == (10 mod 7) * (12 mod 7) mod 7
   (7 * 17 = 119)
3. if x mod z == 1, then xⁿ mod z == 1
   Example: 8 mod 7 == 1, and 8² mod 7 == 1
   This is a special case of 2!

So, we have:






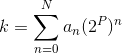
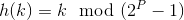
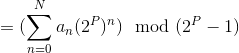
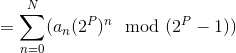  (By 1)

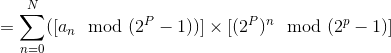  (By 2)

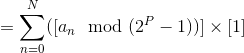  (By 3)

• Establish a family of hash functions.
• Choose so that Prob[h(x) = h(y)] ≤ 1/m, where m is the size of our hash table.
  In other words, the hash functions have no more chance of collision than simply randomly choosing to slots between 1 and m.
• Choose one at random each execution.
  Tricky: what if we store hash values?
• Good average case behavior
  If a "bad" function handles some data once, a "good" one will handle it another time.
  So a "bad" set of programming variable names one run will turn into a good set the next run.