Design and Analysis of Algorithms: Heapsort

Heaps are used in many famous algorithms such as:

• Dijkstra's algorithm for finding the shortest path
• The heapsort sorting algorithm
• Implementing priority queues

Essentially, heaps are the data structure you want to use when you want to be able to access the maximum or minimum element very quickly.There are many variations of heaps, each offering advantages and tradeoffs.
Definition
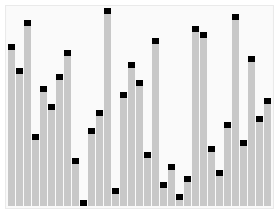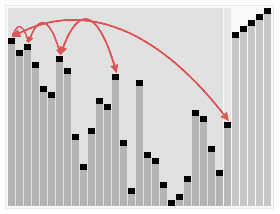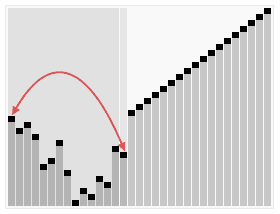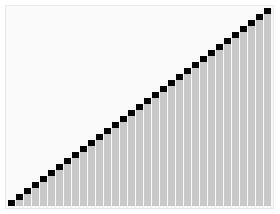
The (binary) heap data structure is an array object that we can view as a nearly complete binary tree as shown in the figure below.Each node of the tree corresponds to an element of the array. The tree is completely filled on all levels except possibly the lowest, which is filled from the left up to a point.

A heap data structure (not garbage-collected storage) is a nearly complete binary tree.

• Height of node = # of edges on a longest simple path from the node down to a leaf.
  
• Height of heap = height of root = (lg n). A heap can be stored as an array A.
  
• Root of tree is A[0].
  
• Parent of A[i] = A[⌊i/2⌋].
  
• Left child of A[i] = A[2i ].
  
• Right child of A[i] = A[2i + 1].
  

Heapify picks the largest child key and compare it to the parent key. If parent key is larger, then heapify quits, otherwise it swaps the parent key with the largest child key. So that the parent is now becomes larger than its children. It is important to note that swap may destroy the heap property of the subtree rooted at the largest child node. If this is the case, Heapify calls itself again using largest child node as the new root.

Heapify(A, i)
  l = left [i]
  r = right [i]
  if l ≤ heap-size [A] and A[l] > A[i]
     largest = l
  else largest = i
  if r ≤ heap-size [A] and A[r] > A[largest]
     largest = r
  if largest != i
     exchange A[i] with A[largest]
     Heapify (A, largest)



1. The max heap property means that
1. a node can't have a greater value than its parent
2. a node must have a value equal to its parent
3. a node can't have a lesser than its parent
4. all values must be heaped up in one node
2. In a max-heap, element with the greatest key is always in the which node?
1. first node to the right
2. root node
3. first node to the left
4. leaf node
3. What is the complexity of adding an element to the heap.
1. O(nlogn)
2. o(n^2)
3. O(logn)
4. O(n)

The heap sort algorithm starts by using procedure BUILD-HEAP to build a heap on the input array A[1 . . n]. Since the maximum element of the array stored at the root A[1], it can be put into its correct final position by exchanging it with A[n] (the last element in A). If we now discard node n from the heap than the remaining elements can be made into heap. Note that the new element at the root may violate the heap property. All that is needed to restore the heap property.

HEAPSORT(A)
  BUILD-MAX-HEAP(A)
  for i = A.length downto 2
      exchange A[1] with A[i]
      A.heap-size = A.head-size - 1
      MAX-HEAPIFY(A, 1)


The HEAPSORT procedure takes time O(n lg n), since the call to BUILD_HEAP takes time O(n) and each of the n -1 calls to Heapify takes time O(lg n).

According to wikipedia: A Priority queue is an abstract data type which is like a regular queue or stack data structure, but where additionally each element has a "priority" associated with it.

Simply priority queue is an extension of queue with the following properties.
1) Every item has a priority associated with it.
2) A high priority element is dequeued before an element with low priority
3) If two elements have the same priority, they are served according to their order in the queue

Although heapsort is an excellent algorithm, a good implementation of quicksort will beat heapsort in practice. The heap data structure has a lot of varied use but it is most popularly used to implement priority queues.

Heapa are generally preferred for priority queue implementation because heaps provide better performance when compared to priority queues implemented using arrays or linked list. In a Binary Heap, heap-maximum() can be implemented in O(1) time, insert() can be implemented in O(lg n) time and extract-maximum() can also be implemented in O(lg n) time as compared to O(n) in case of linked list.

A max priority queue is priority queue based on a max heap and supports the following operations:
1) max-heap-insert(A, key) inserts the element x into the heap A while maintaining the heap property.

            max-heap-insert(A, key)
                A.heap-size = A.heap-size + 1;
                A[A.heap-size] = -Inf;  
                heap-increase-key(A, A.heap-size, key);

        Complexity: O(lg N).
            

2) maximum(S) returns the element of S with the largest key.

            maximum(A)
                return A[1]

        Complexity: O(1)
            

3) extract-max(A) removes and returns the element of S with the largest key.

            extract_maximum (A)
                if(A.heap-size < 1)
                    error("Cannot remove element as queue is empty");
                int max = Arr[1];
                Arr[1] = Arr[length];
                length = length -1;
                max_heapify(Arr, 1);
                return max;
            }

        Complexity: O(lg n)
            

4) increase-key(A, x, k) increases the value of element x's key to the new value k, which is assumed to be at least as large as x's current key value.

            increase-key (A, x, key) {
                if(key < A[i]) {
                    error("New value is less than current value, can't be
                            inserted");
                }
                A[i] = key;
                while( i > 1 and A[i/2] < A[i]){
                    swap(A[i/2], A[i]);
                    i = i/2;
                }
            }

        Complexity: O(log N).
            

Some of the applications of the priority queues are as follows

1) Schedule jobs on a shared computer: We can use max-priority queues to schedule jobs on a shared computer. The max-priority queue keeps track of the jobs to be performed and their relative priorities. When a job is finished or interrupted, the scheduler selects the highest-priority job from among those pending by calling EXTRACT-MAX. The scheduler can add a new job to the queue at any time by calling INSERT.
2) Event driven simulator: A min-priority queue can be used in an event driven simulator.The items in the queue are events to be simulated, each with an associated time of occurrence that serves as its key. The events must be simulated in order of their time of occurrence, because the simulation of an event can cause other events to be simulated in the future
3) Graph Search Algorithms: Many efficient graph search algorithms such as A* search and Dijkstra's algorithm use priority queues to know which nodes to explore next.
4) Bandwidth Management: Priority queues are used to handle data flows on the network. As not all data are of same importance by prioritizing the important data packets the router can make sure that the network performs optimally and all the prioritized traffic is forwarded with the least delay and the least likelihood of being rejected in case of the router reaching its max traffic capacity.