Note: ^ means “raise to the power”.
1.(4 points) Use your own words to illustrate in what scenarios we should use greedy algorithm or dynamic programming. Please give examples of when each paradigm works. (For example, we can apply dynamic programming on rod cutting, greedy algorithm cannot work here because rod cutting needs to use sub-rob-cutting cases to calculate final result. Use example outside course material or try to illustrate in general way)
Sample Answer: For example, we can apply dynamic programming on rod cutting, greedy algorithm cannot work here because rod cutting in one place can prevent us from taking the optimal solution in another place. For instance, if we cut an 8-foot rod in half, we can't make a 5-foot cut if that turns out to be better.
2. (2 points) Greedy algorithms are also used widely in memory management. Given a list of blocks, in which the sizes are { 100, 150, 180, 200, 300 }, how would a greedy algorithm (grab the smallest block that works first) fit processes with sizes {10, 222, 198, 147, 178 }?
a. process 1: block 1, process 2: block 2, process 3: block 4, process 4: block 3, process 5: block 5
b. process 1: block 1, process 2: block 5, process 3: block 4, process 4: block 3, process 5: block 2
c. process 1: block 5, process 2: block 2, process 3: block 4, process 4: block 3, process 5: block 1
d. process 1: block 1, process 2: block 5, process 3: block 4, process 4: block 2, process 5: block 3
Answer: d. process 1: block 1, process 2: block 5, process 3: block 4, process 4: block 2, process 5: block 3
3.(2 points) Which of the following is/are property/properties of a dynamic programming problem?
a. Optimal substructure
b. Overlapping subproblems
c. Greedy approach
d. Both optimal substructure and overlapping subproblems
Answer: d. Both optimal substructure and overlapping subproblems
4. (2 points) If a problem can be broken into subproblems which are solved several times, the problem possesses ____________ property.
a. Overlapping subproblems
b. Optimal substructure
c. Memoization
d. Greedy
Answer: a. Overlapping subproblems
Reason: In computer science, a problem is said to have overlapping subproblems if the problem can be broken down into subproblems which are reused several times or a recursive algorithm for the problem solves the same subproblem over and over rather than always generating new subproblems
5. (1 point) When dynamic programming is applied to a problem with overlapping subproblems, the time complexity of the resulting program typically will be significantly less than a straightforward recursive approach.
Answer: True
Reason: The overlapping subproblems are not solve again and again. We follow a memozied approach which result in a memory-time trade-off. It results in reducing the complexity of the algorithm to a very large extent
6. (2 points) In dynamic programming, the technique of storing the previously calculated values is called ___________
a. Saving value property
b. Hashing
c. Memoization
d. Mapping
Answer: c. Memoization
Reason: It memorizes or stores the results for subproblems.
7. (4 points) Modify MEMOIZED-CUT-ROD from the textbook to return not only the value but the actual solution too.
Answer:
EXTENDED-BOTTOM-UP-CUT-ROD(p,n)
1. let r[0..n] and s[0..n] be new arrays
2. r[0] = 0
3. for j = 1 to n
4. q = -INF
5. for i = 1 to j
6. if q < p[i] + r[j-i]
7. q = p[i] + r[j-i]
8. s[j] = i
9. r[j] = q
10. // Print optimal cuts
11. i = n
12. while i > 0
13. print s[i]
14. i = i - s[i]
15. return r and s
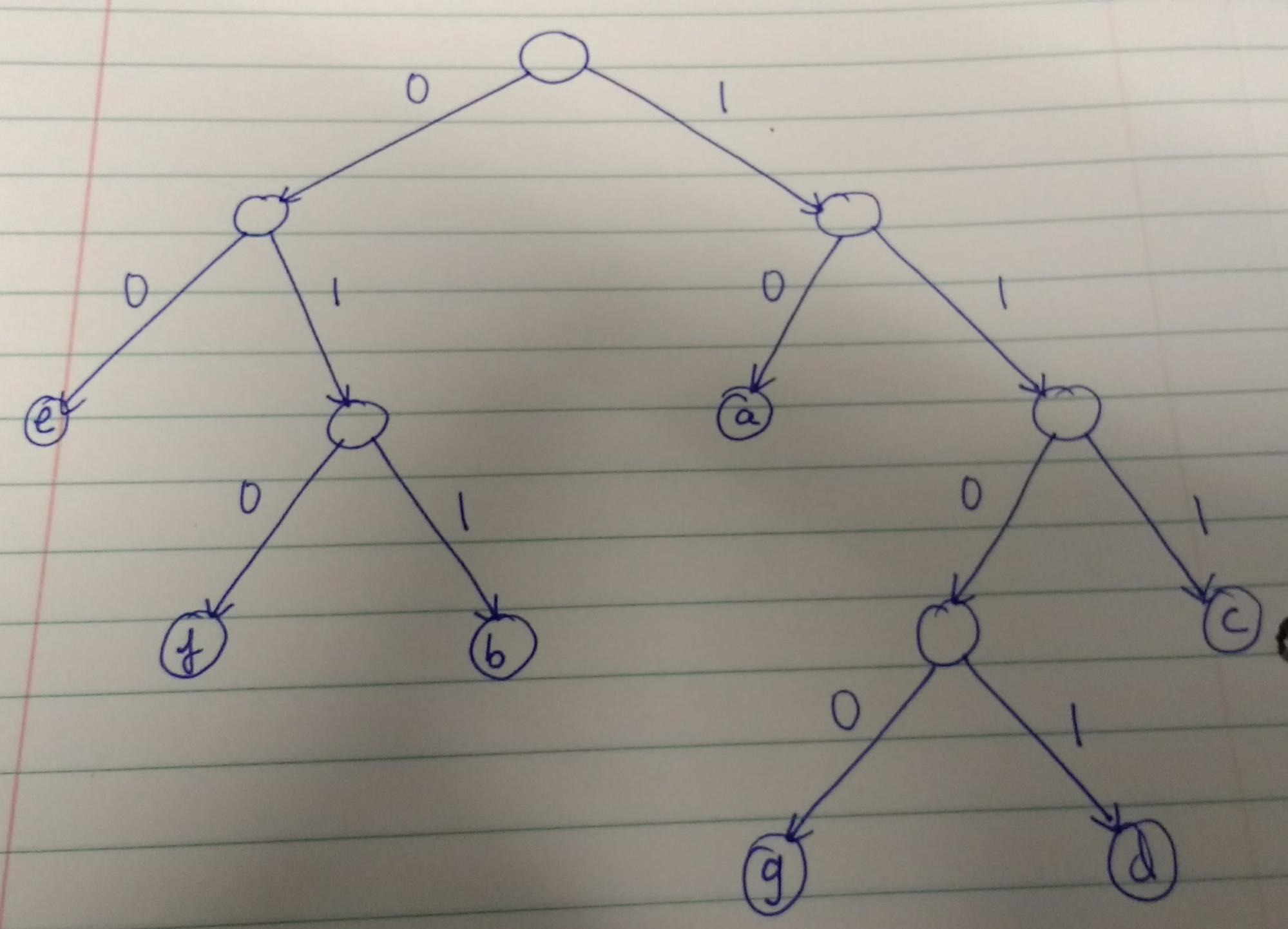
8. (4 points) Describe the Huffman encoding that will deal with the following letters and their corresponding frequencies.
(g, 6), (d,13), (f,17), (b,18), (c, 29), (e, 30), (a, 37)
Answer:
(It’s not necessary to draw a tree although it is preferable)
a -> 10
b -> 011
c -> 111
d -> 1101
e -> 00
f -> 010
g -> 1100
9. (2 points) Huffman’s algorithm is a greedy algorithm because:
a. The frequencies are combined at each step
b. The two smallest probability nodes are chosen at each step
c. It involves drawing a Huffman tree
d. Both a and c.
Answer: b. The two smallest probability nodes are chosen at each step
Explanation: Satisfies greedy property.
10. (2 points) A thief enters a store and sees the following items: Bag A worth $100 weighing 2 pounds, Bag B worth $10 weighing 2 pounds and Bag C worth $120 weighing 3 pounds. His Knapsack holds 4 pounds. What is his maximum profit according to the Fractional Knapsack Problem?
a. 120
b. 195
c. 180
d. None of the above
Answer: c. 180
Explanation: In the Fractional Knapsack problem, the item with the maximum ‘by weight’ profit is chosen first. In this case the maximum ‘by weight’ profit is obtained by choosing Bag A (100/2 is equal to 50).
Current Profit: 100
Bag A weighs 2 pounds so there are 2 more pounds remaining in the Knapsack. The next maximum ‘by weight’ profit is Bag C (120/3 is equal to 40). So we take 2 pounds of Bag C.
Final profit: 100+(2*40) = 180
11. (2 points) You are building up a new housing subdivision (community / neighborhood). You have picked out a series of good house sites 1 kilometer apart from each other. However, zoning regulations in this very rural area require that each house be 4 kilometers from any other house. Given you have a list, r, of the revenue you expect from each site (they differ because of the view!), what is the recurrence relation you should use to pick out the maximum revenue you can expect from the entire development?
a. T(n) = r-sub-n + T(n - 4)
b. T(n) = max(r-sub-n, T(n - 4))
c. T(n) = max(r-sub-n + T(n - 4), T(n - 1))
d. T(n) = max(r-sub-n + T(n - 1), T(n - 4))
Answer: c. T(n) = max(r[n] + T(n - 4), T(n - 1))
Reason: Because it accurately captures the problem!
12. (4 points) The Lucas series is similar to the Fibonacci series, except that its base cases are L(0) = 2 and L(1) = 1. Please write memoized code for computing the n-th Lucas number. (Pseudo-code is fine here, but you can also write code in any common language like C, Java, Python, Ruby, etc.)
Answer:
Just like memo_fib, except for 0 we return 2, and 1 we return 1.
def memo_fib(n, first_call=True): | |
""" | |
A memo-ized version of naive fib, that runs much faster. | |
Args: | |
n: the fibonacci number to return | |
first_call: Is this the top-level call to this function? | |
Returns: | |
The n-th fibonacci number. | |
""" | |
global ops | |
global results | |
if first_call: | |
ops = 0 # make sure we don't count some other call's operations! | |
results = [-1 for x in range(1000)] | |
if n < 0: | |
print("n must be >= 0!") | |
return -1 | |
elif n == 0: | |
ops += 1 | |
return 0 | |
elif n == 1: | |
ops += 1 | |
return 1 | |
else: | |
# Here we check and see if we have calculated the results | |
# we need earlier. If so, use them. If not, calculate and | |
# then store ("memo-ize") them. | |
n_minus_one = 0 | |
n_minus_two = 0 | |
if results[n - 1] >= 0: | |
ops += 3 # if, assignment, and subtraction | |
n_minus_one = results[n - 1] | |
else: | |
ops += 5 # two assignments, two subtractions, function call | |
n_minus_one = memo_fib(n - 1, False) | |
results[n - 1] = n_minus_one | |
if results[n - 2] >= 0: | |
ops += 3 # if, assignment, and subtraction | |
n_minus_two = results[n - 2] | |
else: | |
ops += 5 # two assignments, two subtractions, function call | |
n_minus_two = memo_fib(n - 2, False) | |
results[n - 2] = n_minus_two | |
ops += 1 | |
return n_minus_one + n_minus_two | |
13. (4 points) Suppose you were to drive from St. Louis to Denver along I-70. Your gas tank, when full, holds enough gas to travel m miles, and you have a map that gives distances between gas stations along the route. Let d1 < d2 <... < dn be the locations of all the gas stations along the route where d-sub-i is the distance from St. Louis to the gas station. You can assume that the distance between neighboring gas stations is at most m miles. Your goal is to make as few gas stops as possible along the way.
Give the most efficient algorithm you can find to determine at which gas stations you should stop and prove that your strategy yields an optimal solution. Be sure to give the time complexity of your algorithm as a function of n.
(Pseudo code expected.)
Answer:
14. (2 points) An example of set of coin denominations for which the greedy algorithm does not yield an optimal solution is {_________________}.
Answer: { 1, 3, 4 } for 6 as change amount with minimum number of coins
It will give the answer 4 + 1 + 1
Whereas the correct answer is 3 + 3
Note: The answer for this question may differ from person to person.
15. (3 points) Explain why the time complexity of Huffman coding is O(n lg n) (this could be a full formal proof, but a good intuitive explanation is sufficient)?
Answer: For each of n items we do at most lg n operations to get it at the right place in the tree.