Design and Analyis of Algorithms: Minimum Spanning Trees

Overview

Tree: A connected graph with no cycles.
Given a graph G, any tree that includes all of the vertices of G is called a spanning tree. The lowest-weight tree that does that is a minimum spanning tree.

These are used to solve problems such as:

Lowest cost way to bring a package between two cities.
Most efficient way to connect two components on a circuit board.
Most efficient way to connect two strangers in a social network.

This problem can be solved using a greedy algorithm.

It runs on a weighted graph. (On an unweighted graph, all spanning trees are minimal: tree property E = V - 1.)

The Generic MST Algorithm

Generic-MST(G, w)
A = ∅
while A does not form a spanning tree
fine an edge (u, v) that is safe for A
A = A ∪ {(u, v)}
return A

Loop invariants:

Finding a "safe" edge

How do we find a safe edge?
One must exist, since we are working with a connected graph, and A is at all times a part of an MST.
Definition: a cut (S, V - S) of an undirected graph G = (V, E) is a partition of V.
Definition: an edge (u, v) crosses the cut (S, V - S) if one of its endpoints is in S and the other in V.
Definition: a cut respects a set A of edges if no edge in A crosses the cut.
Definition: An edge is a light edge crossing a cut if its weight is minimum among all edges crossing the cut. Uniqueness is not required.

Kruskal's Algorithm

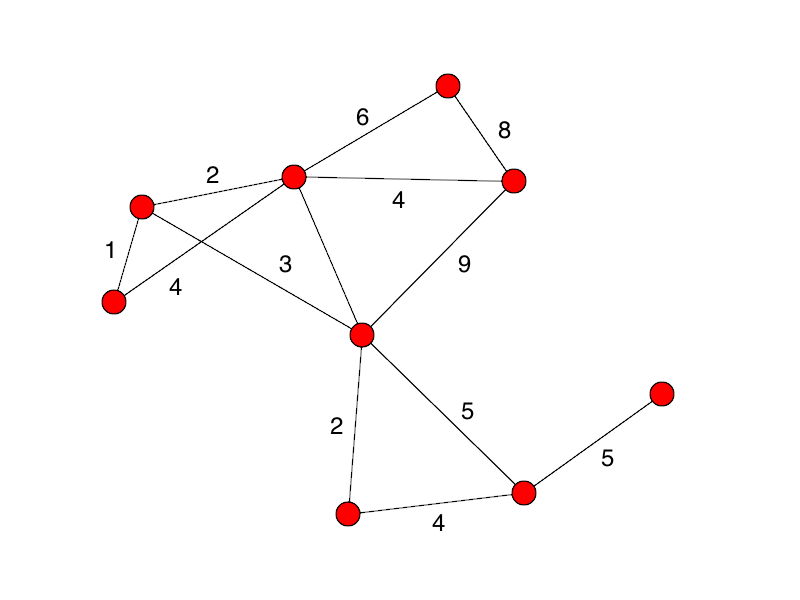
We add edges in increasing-cost order, so long as the edges don't create a cycle (are "safe").
Steps:

Include the edge weighted 1.
Include both edges weighted 2.
Include the edge weighted 3.
Include the upper and lower edges weighted 4. (Not the middle one!)
Include the lone edge weighted 5.
Include the edge weighted 6.

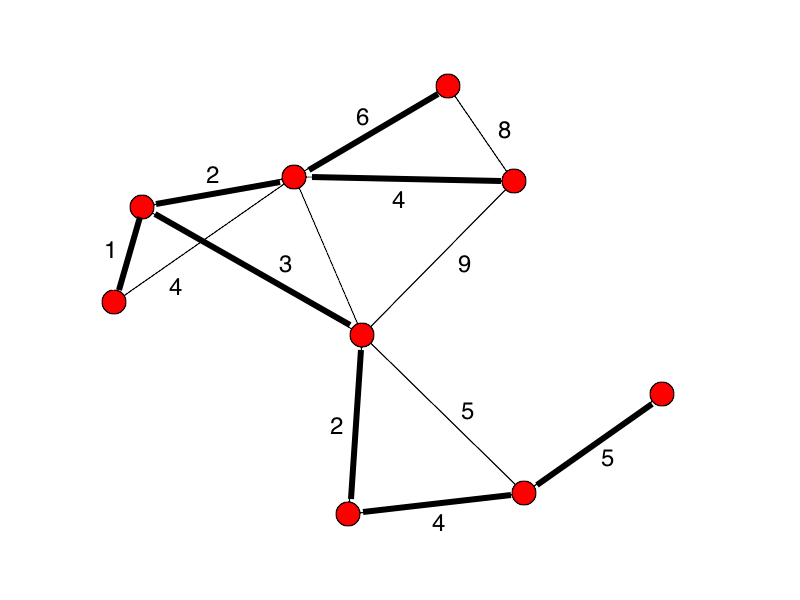
Proof: Is Kruskal's algorithm guaranteed to always find the minimum spanning tree?
Yes, it is. Let's prove it.
We suppose that graph G has n vertices. Then our algorithm will create a tree T with edges e₁, e₂, ... e_{n - 1}, where w(e₁) ≤ w(e₂) ≤ ... w(e_{n - 1}).
Suppose that there is a tree T* with a lesser weight.
Let e_k be the first edge in T that is not in T*.
Now we insert e_k in T*. This will produce a cycle in T*, by the nature of trees. There must be some edge e^* that is in T* but not in T (otherwise T would have a cycle).

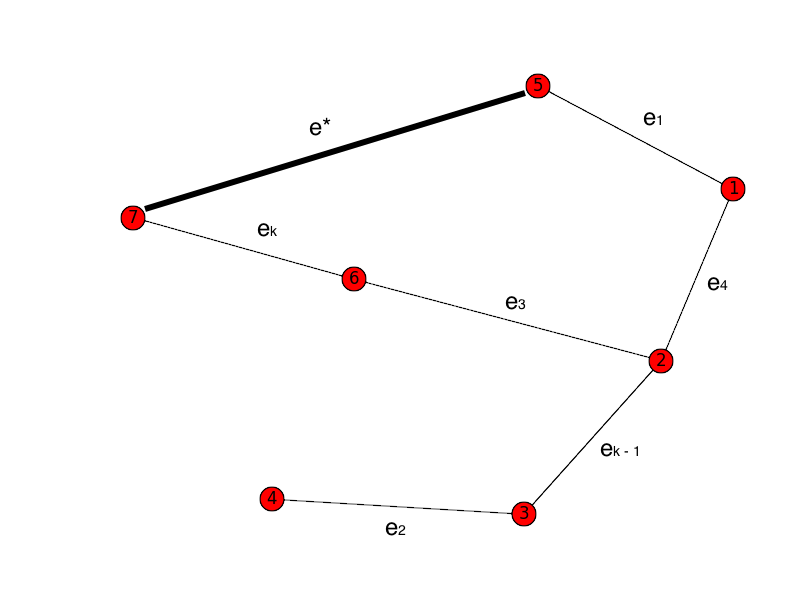
But the weight of e_k must be less than the weight of e^*, because after we had inserted e₁ through e_{k - 1}, we could have next chosen e^*... but we did not. Instead we chose e_k.
So T* does not have a lesser weight after all.

How to find safe edges

Place each vertex in its own set. (We now have a forest of one-vertex, unconnected trees.)
We examine edges (u, v) in non-decreasing order.
If u and v are not in the same set (tree), add the edge. (It is safe.)
If u and v are in the same set, adding the edge would create a cycle (by the nature of trees, E = V - 1).

Prim's Algorithm

The big difference from Kruskal: in Kruskal, we have a set of edges, perhaps with no connections, that eventually turns into a tree.
With Prim, we continually have an ever-growing tree. In fact, it is always an MST of a sub-graph of our graph.

Source Code

Python