Randomized Algorithms


The hiring problem

Here's the algorithm: 

                Hire-Assistant(n)
                    best = 0
                    for i = 1 to n
                        interview candidate i
                        if i is better than best
                            best = i
                            hire(i)

Worst-case analysis

The worst case: the employment agency sets us up, and sends us candidates in worst-to-best order, so we hire every single one.

Probabilistic anaysis

We use probability theory to find an average-case running time. This is the average over some likely distribution of inputs.
If we don't know our likely inputs, we can't use probabilistic analysis.

See also: Probability basics.

A randomized algorithm

We best the employment agency by shuffling their list of candidates, and seeing them in random order: we get a much lower average cost, as we shall prove.

An algorithm is randomized if its behavior is controlled not only by its inputs but also by a random-number generator .
Random(m, n) returns with equal probability an integer between m and n inclusive. So Random(2, 4) returns either 2, 3, or 4, each with probability 1/3.

When we randomize the algorithm we speak of an expected running time.
Average-case running time: the probability distribution is over inputs.
Expected running time: the algorithm itself makes random choices.

Indicator random variables

(Note: random variables are actually functions.)

X is an indicator variable for an event A if:

Useful properties of indicator variables

If X is an indicator variable for A, then

Exp[X] = Prob[X=1] = Prob[A happens]

This easily follows from the definition:

Exp[X] = 1 * Prob[X=1] + 0 * Prob[X=0] = Prob[X=1] = Prob[A happens]

Example:

We throw a fair die 100 times What is the expected number of times we get 1 or 6?

Let Xi be the indicator variable of the event "in ith throw we got 1 or 6". Then notice that the number of times we get 1 or 6 is:



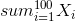
and we want the expectation of this. By linearity of expectations:



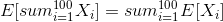
and by the indicator variable properties:



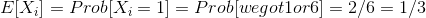
To summarize:



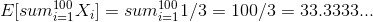
So we expect to get 1 or 6 about 33.33 times.

Analysis of hiring problem using indicator random variables

The first candidate we always hire. The second candidate will be better half the time, the third one will be better than the first two one third of the time, and so on, so we get the series:
1 + 1/2 + 1/3 + 1/4...
(Or y = 1/x.)

So:






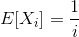
(By linearity of expectations.)





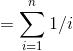
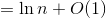
Why is the last step true? Video here.

Basically, the anti-derivative of 1/x is ln x:

Randomized algorithms

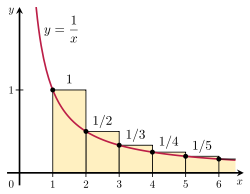
In average-case analysis, we consider run-time over a probability distribution of inputs.
So, for Hire-Assistant, if we get candidates in order (with higher numbers meaning better):
A1 = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
we hire all 10 candidates. If we get:
A2 = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
we hire only once. And if our input is:
A3 = [5, 2, 1, 8, 4, 7, 10, 9, 3, 6]
we hire three times. So A1 is very expensive input, A2 is very cheap, and A3 is in between.

On the other hand, if we have a randomized algorithm, we can't say anything about how "good" A1, A2, and A3 are as inputs: they are randomized before the hire code runs. No particular input elicits worst-case behavior.

Randomly permuting arrays 

                 Permute-By-Sorting(A)
                    n = A.length
                    let P[1..n] be a new array
                    for i = 1 to n
                        P[i] = Random(1, n^3)
                    sort A, using P as sort keys

We cube n to get at least 1 - 1/n^3 probability that all enties are unique.

Run the Python code for the randomized algorithm to hire an assistant

In the console below, type or paste:
!git clone https://gist.github.com/91e59d2a36937f9be17cee01ddb9588d.git
cd 91e59d2a36937f9be17cee01ddb9588d
from hire_assistant import *
n=18
hire_assistant(n,False)

Python console

Now you can experiment with the algorithm by changing the value of n and running hire_assistant(n, False)

Probabilistic analysis and further uses of indicator random variables
The birthday paradox




Probability that two people have the same birthday: 1/365

To generalize the problem, and see it doesn't just apply to birthdays, let's call the # of days in the year n.

Let's set up an indicator random variable so that Xij is: 1 if persons i and j have the same birthday.
0 if the don't.

Let X count the number of pairs of people who have the same birthday.

k is the number of people in the room.



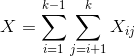
Take expectations and apply linearity of expectation:









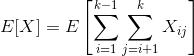
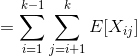
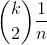
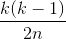
So we need:
k2 ≥ 2n
For 365 days in a year, square root of 730 ≈ 27.
So we are looking at Θ(n1/2), asymptotically speaking.

Balls and bins

b: number of bins.
n: number of balls.
Expected balls in a given bin?: n / b
Expected tosses until a given bin contains a ball?: b
How many balls must we toss until we expect that every bin contains at least one ball?
Call a ball falling in an empty bin a "hit."
First toss is a guaranteed hit!
For the next stage, we have i - 1 bins containing balls, and b - i + 1 bins empty.
So for ith stage, the probability of a hit is:
(b - i + 1) / b So, for 6 bins, the expected tosses to fill the next bin are:
E(n2) = 6 / 5
E(n3) = 6 / 4
E(n4) = 6 / 3
(Some math equations to be filled in!)
And we get b ln b for the expected number of tosses until each bin has at least one ball in it.

Streaks
NOT COVERED FALL 2017
The on-line hiring problem
NOT COVERED FALL 2017

Source Code

Java
Ruby
C++
Python