Design and Analysis of Algorithms: Red-Black Trees

1. Every node is red or black.
2. The root is black.
3. Every leaf (T.nil) is black.
4. If a node is red, then both of its children are black. (Never two reds in a row while descending!)
5. For each node, all paths from the node to its descendant leaves contain the same number of black nodes.

T.nil: This is simply a space saving device: every "leaf" node of an ordinary BST gets left and right child pointers to a special node, T.nil, and the root node of the tree has its parent point to this as well.

How Red-Black Trees Solve the BST Problem

And so, a simple way to get an intuition as to why no leaf is further than twice as far from the root as the nearest leaf: The nearest leaf at the least bh levels from the root. (The black-height of every node is the same.) Since there is never more than one R-node between any two B-nodes, at most, the furthest node can be 2B levels away from the root.
So we get:
A red-black tree with n internal nodes has height at most 2 lg(n + 1).

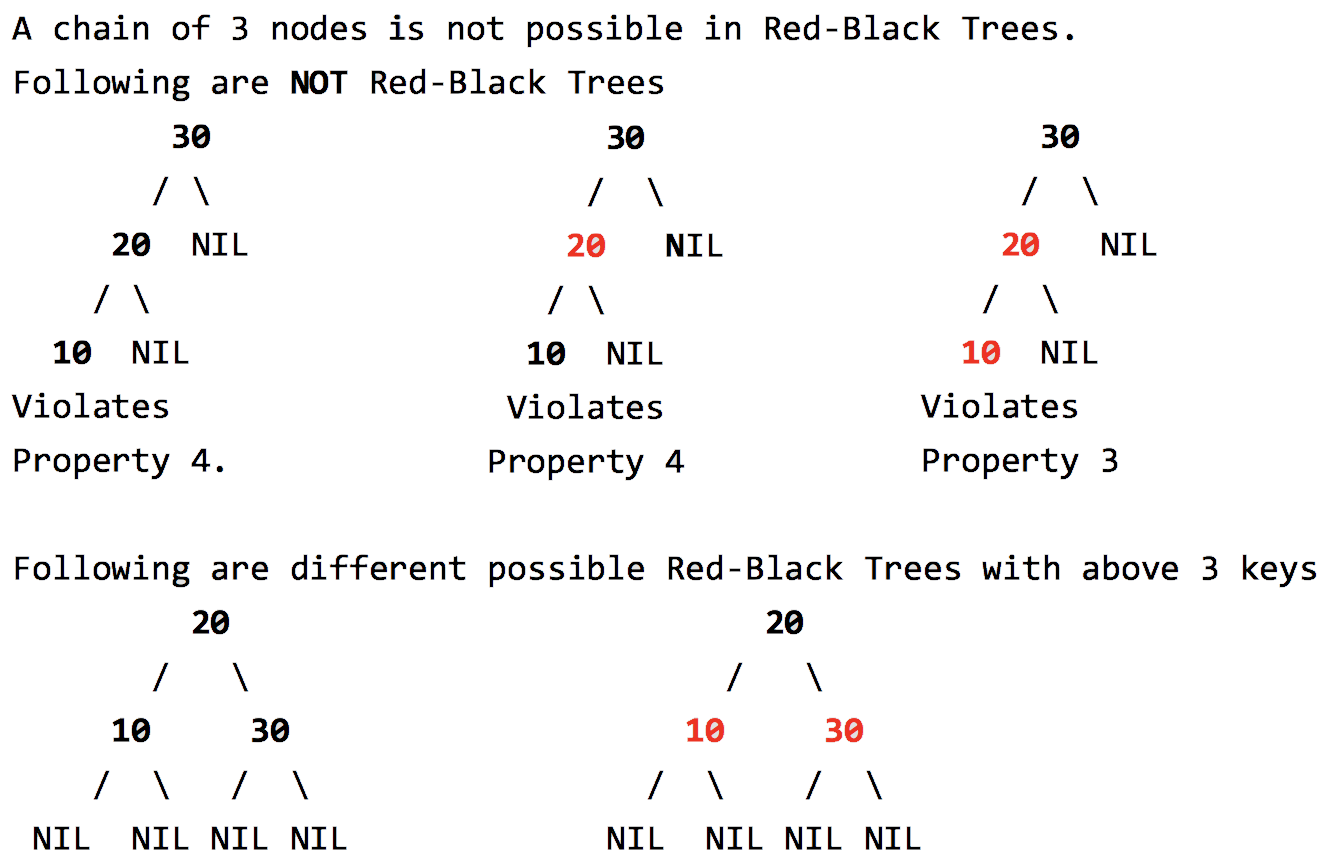
Remember: This is a binary search tree.
So, non-modifying operations such as minimum(), maximum(), successor(), predecessor(), and search() run in O(height) time, and so for red-black trees, in O(lg n) time.

But what about insert and delete? They are obviously trickier. In fact, they are the whole trick: the red-black properties are just a way of keeping the tree roughly balanced.

But to get to insert and delete, we need to pass through rotations on the way.

1. The maximum height for a red-black tree is
1. n
2. 8lg(n + 1)
3. lg(n)
4. 2lg(n + 1)
2. A red-black tree is
1. a type of binary search tree
2. a minimum spanning tree
3. a B-tree
3. The goal of red-black trees is to
1. keep a BST balanced
2. minimize insert time in a BST
3. minimize delete time in a BST
4. minimize search time in a BST
4. Given the properties of a red-black tree, one can never have
1. a root node that is black
2. nil leaf nodes
3. two black nodes linked
4. two red nodes linked

Let's enter 6, 4, 2 in the:
Red-black tree visualizer

Note: In-order walks of the pre- and post-rotate trees produce the same output. It is still a BST!

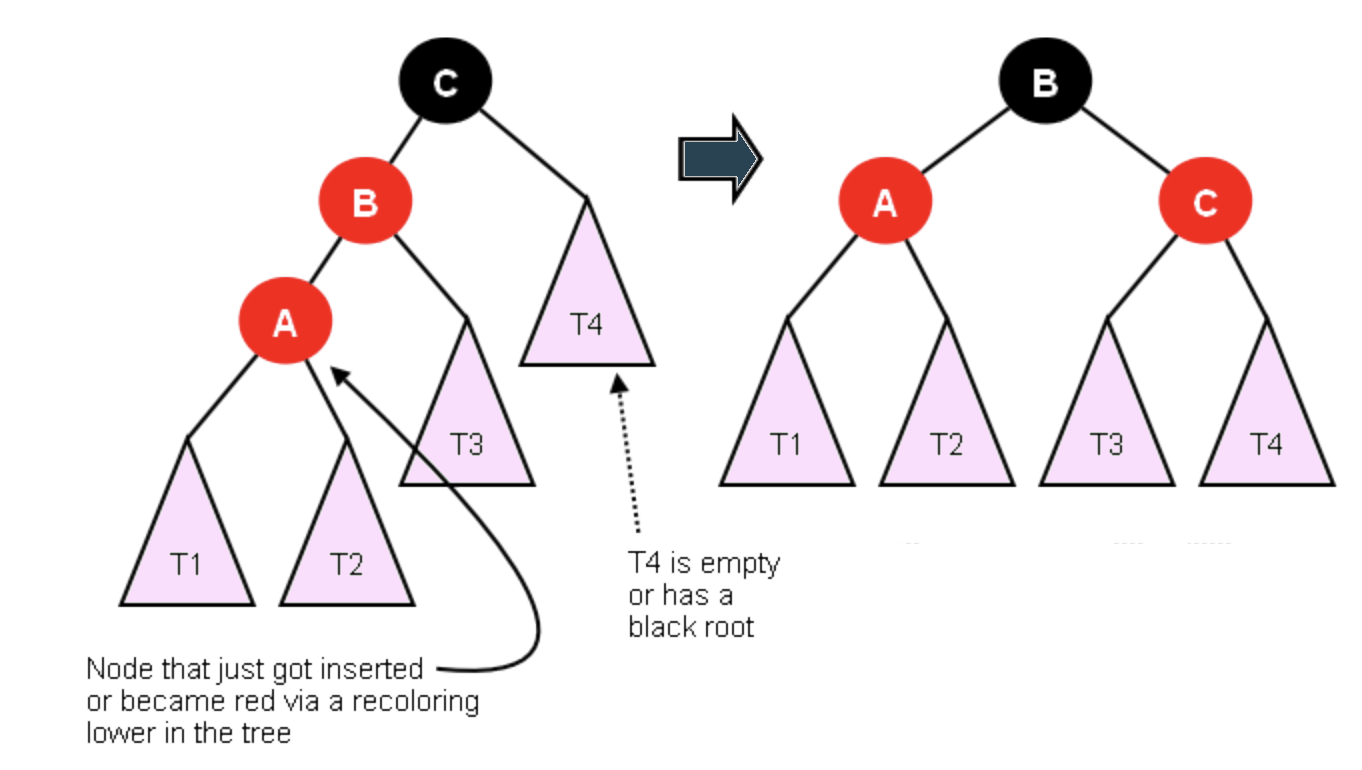
Let's enter 2, 4, 6 in the:
Red-black tree visualizer

Here's the pseudo-code:

                Left-Rotate(T, x)
                    y = x.right
                    x.right = y.left
                    if y.left != T.nil
                        y.left.p = x
                    y.p = x.p
                    if x.p == T.nil
                        T.root = y
                    elif x == x.p.left
                        x.p.left = y
                    else
                        x.p.right = y
                    y.left = x
                    x.p = y
                

Here's the pseudo-code:

                RB-Insert(T, z)
                    y = T.nil
                    x = T.root
                    while x != T.nil
                        y = x
                        if z.key < x.key
                            x = x.left
                        else
                            x = x.right
                    z.p = y
                    if y == T.nil
                        T.root = z
                    elseif z.key < y.key
                        y.left = z
                    else
                        y.right = z
                    z.left = T.nil
                    z.right = T.nil
                    z.color = RED
                    RB-Insert-Fixup(T, z)
                

                RB-Insert-Fixup(T, z)
                    while z.p.color == RED
                        if z.p == z.p.p.left
                            y = z.p.p.right
                            if y.color == RED
                                z.p.color = BLACK
                                y.color = BLACK
                                z.p.p.color = RED
                                z = z.p.p
                            else
                                if z == z.p.right
                                    z = z.p
                                    Left-Rotate(T, z)
                                z.p.color = BLACK
                                z.p.p.color = RED
                                Right-Rotate(T, z.p.p)
                        else // same as if with right and left reversed
                            ...
                    T.root.color = BLACK
                

1. Node z is red.
2. If z.p is the root, then z.p is black.
3. If the tree violates any red-black properties, then it violates at most one. That one will be either:
   • Property 2, because z is the root and is red, or
   • Property 4, because z and z.p are both red.

Each loop iteration we do one of two things: either we move up the tree,

The insert code itself (without fixup) takes O(lg n) time, just like for a BST.
In fixup, the rotations occur in constant time.
We move up the tree while fixing, and this happens at most lg n times.
Therefore, insert is O(lg n).

1. Why do we left rotate at line 12 of RB-Insert-Fixup?
1. z is its parent's left child, which means the tree is growing to the left
2. because z's parent is the right child of z's grandparent
3. because z's grandparent is RED
2. Line 4 of RB-Insert-Fixup, where the color of y is checked, is determining
1. the color of z's niece
2. the color of z's grandparent
3. the color of z's uncle
4. the color of z's parent

• Red node
• Black node with red child
• Black node with black children

RB-Delete is going to rely on RB-Transplant:

                    RB-Transplant(t, u, v)
                        if u.p == T.nil
                            T.root = v
                        elsif u == u.p.left
                            u.p.left = v
                        else
                            u.p.right = v
                        v.p = u.p
                    

And this will only be called on nodes for which it will work: we don't call it on a node with two children asking that one of them be its replacement without finding a min or max, for instance.
So here is RB-Delete:

                    RB-Delete(T, x)
                    

And here is RB-Delete-Fixup:

                    RB-Delete-Fixup(T, x)