Design and Analysis of Algorithms Final

Name: _______________________________________

NYU NetID: __________________________________

Multiple Choice

1. Employing the master theorem, the solution to the recurrence T(n) = 2T(n/4) + n^0.51 is
   1. Θ(n²)
   2. Θ(n² log n)
   3. Θ(n^0.51) *
   4. the master theorem can't be applied here.
   
   
2. When we have an optimal substructure and only the locally optimal choice matters, we should probably use:
   1. a straightforward recursive solution.
   2. dynamic programming.
   3. a memoized recursive algorithm.
   4. a greedy algorithm. *
   
   
3. If we have a binary search tree of height h, then all searching functions such as min, max, and successor will run in
   1. O(h²) time.
   2. O(ln h) time.
   3. O(h) time. *
   4. O(lg h) time.
   
   
4. A depth-first search of this tree:
   
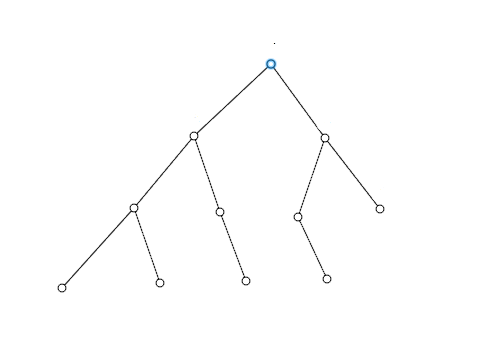
   Will cover the nodes in what order?
   1. A-C-B-H-E-F-I-K-G-J-D
   2. A-B-H-C-F-I-K-D-E-G-J
   3. A-B-C-D-E-F-G-H-I-J-K
   4. A-B-C-H-F-I-K-D-E-G-J
   
   
5. According to the binary search tree property
   1. for all nodes higher in the tree than x, x.key ≤ y.key.
   2. for all nodes in the left subtree of x, y.key ≤ x.key. *
   3. for all nodes lower in the tree than x, x.key ≤ y.key.
   4. all nodes in the right subtree of x will be the successors of x.
   
   
6. Employing the master theorem, the solution to the recurrence T(n) = 0.25T(n/2) + 8n is
   1. Θ(n^-2)
   2. Θ(n^-2 log n)
   3. Θ(8n)
   4. the master theorem can't be applied here. *
   
   
7. For large n, an algorithm will run the slowest if it time complexity is:
   1. O(n³)
   2. O((1.02)ⁿ) *
   3. O(n⁵)
   4. O(500n log n)
   
   
8. Matroids are essentially a theory of
   1. independence. *
   2. connectivity.
   3. resilience.
   4. linearity.
   
   
9. Consider the following alphabet with frequencies:

   Symbol	Frequency
   A	24
   B	12
   C	10
   D	8
   E	8

   Which of the following is a possible Huffman coding for the string "ABBCDAED"?

   1. 11111101011100111110
   2. 11001001011100111110
   3. 01001001011100111110 *
   4. 11001001011100111110
   
   
10. When we have an optimal substructure and overlapping sub-problems, we should probably use:
    1. a straightforward recursive solution.
    2. dynamic programming. *
    3. a merge sort.
    4. a greedy algorithm.
    
    
11. Employing the master theorem, the solution to the recurrence T(n) = 4T(n/2) + cn is
    1. Θ(n²) *
    2. Θ(n² log n)
    3. Θ(cn)
    4. the master theorem can't be applied here.
    
    
12. We have one algorithm for processing customer records with run time of O(n), and another with run time of O(lg n) + 2500.
    In what circumstances might we want to choose the O(n) algorithm?
    1. The algorithm will be distirbuted across a network.
    2. We believe our program will always be dealing with a number of records less than 2500. *
    3. We are running on a slow CPU.
    4. If n is very large.
    
    
13. We can sometimes be loose with our analysis of divide-and-conquer algorithms, in that we might omit details like
    1. recursions and function calls.
    2. exponential factors.
    3. floors, ceilings, and boundary conditions. *
    4. any n raised to a power less than 3.
    
    
14. Under what circumstances might we most reasonably expect to receive worst-case input to our binary search tree?
    1. We insert data into the tree as it comes along to us.
    2. The data has been randomly shuffled.
    3. A user types in the data from a sorted list. *
    4. All of the above.
    
    
15. When we have overlapping sub-problems and we want to solve them from the bottom up, we should employ:
    1. dynamic programming *
    2. a recursive algorithm
    3. a recursive algorithm with memoization
    4. a greedy algorithm
    
    
16. When we randomize an algorithm, we then speak of its
    1. necessary running time.
    2. best-case running time.
    3. expected running time. *
    4. unbounded running time.
    
    
17. For large n, an algorithm will run the fastest if it time complexity is:
    1. O(n!)
    2. O(n³) *
    3. O(n⁴)
    4. O((1.02)ⁿ)
    
    
18. Strongly connected components of a graph are
    1. components of a directed graph that can each be reached from each other. *
    2. components in a weighted graph where the connections have the highest weights.
    3. components of a spanning tree.
    4. an vertices with edges between them.
    
    
19. Which of these functions grows most slowly?
    1. lg n
    2. lg* n *
    3. ln n
    4. log₁₀ n
    
    
20. For a greedy algorithm to work, the optimal choice
    1. must depend on many over-lapping sub-problems.
    2. must not depend on any future choices. *
    3. must be dependent on a global optimal.
    4. must only be available after considering all sub-problems.
    
    
21. Ω-notation applied to a function implies
    1. it is a function we know little about.
    2. it is asymptotically bound from above and below.
    3. only that it is asymptotically bound from below. *
    4. only that it is asymptotically bound from above.
    
    
22. In algorithm analysis, we usually analyze algorithms in terms of
    1. actual running time in nanoseconds.
    2. the number of disk operations.
    3. the number of basic operations. *
    4. CPU time used.
    
    
23. In proving that a problem has the greedy-choice property,
    we often use a proof technique called:
    1. cut-and-paste. *
    2. the master theorem.
    3. substitution.
    4. recursion-tree analysis.
    
    
24. The chief advantage of a doubly-linked list over a singly-linked list is
    1. inserts are faster.
    2. there are fewer pointers to maintain.
    3. we can back up as well as go forward in the list. *
    4. less memory is used.
    
    
25. Often, a good alternative to dynamic programming is
    1. a simple recursive solution.
    2. a recursive solution with memoization. *
    3. a brute-force solution.
    4. all of the above.
    
    
26. A random variable is actually
    1. the mean of all possible values.
    2. an algorithm.
    3. a precise real number value.
    4. a function. *
    
    
27. In the substitution method for solving recurrences, we
    1. substitute a different recurrence for the one characterizing our algorithm.
    2. guess a solution and then use induction to prove it.
    3. substitute a polynomial factor for an exponential one.
    4. substitute an n² wherever we see a 2ⁿ
    
    
28. Consider the following recursion tree.
    
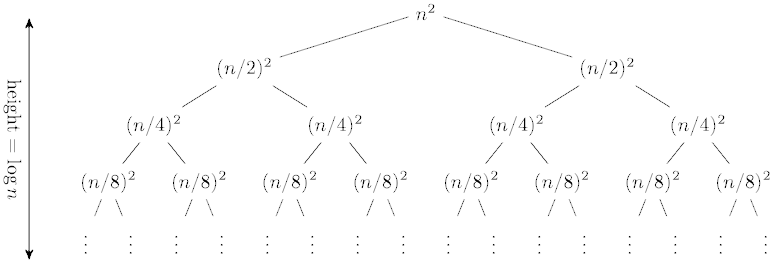
    What closed form best characterizes this tree?
    1. O(n/8)
    2. O(n log n)
    3. O(n²)
    4. O(log n)
    
    
29. The worst case of hashing with chaining occurs when
    1. the input comes in sorted already.
    2. all inputs hash to different values.
    3. the input is purely random.
    4. all inputs hash to the same value. *
    
    
30. Consider this recurrence:
    
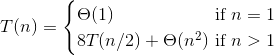
    What is the solution to this recurrence?
    1. T(n) = Θ(n³)
    2. T(n) = Θ(n²)
    3. T(n) = Θ(n⁸)
    4. T(n) = Θ(n^8/3)
    
    
31. If you have available a simple algorithm with some acceptable run time, and a more complex algorithm with slightly faster run time, you should
    1. always choose the faster algorithm.
    2. always choose the simpler algorithm.
    3. consider how big your input is likely to be before choosing either algorithm.
    4. ask your boss what to do.
    
    
32. In graph theory, a tree is
    1. a forest with no edges.
    2. a cyclical graph with no forests.
    3. any walk on a graph.
    4. a connected graph with no cycles.
    
    
33. Graph theory is useful for
    1. task management.
    2. map coloring.
    3. cellular telephone networks.
    4. all of the above.
    
    
34. A problem with linear probing to resolve hash collisions is
    1. the code is extremely complex.
    2. clusters of keys will build up in a linked list.
    3. the hash table clusters around its central value.
    4. once inputs start to cluster in one area of the hash table, they will become more likely to do so. *
    
    
35. Consider this graph:
    
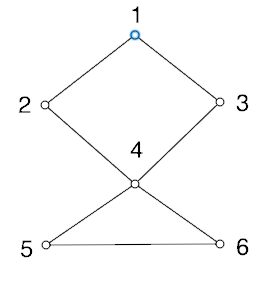
    Which of the following would be an adjacency list representation of this graph?
    1. 1 (2, 3, 4) 2 (1, 4) 3 (1, 4) 4 (2, 3, 5) 5 (4, 6) 6 (4, 5)
    2. 1 (2, 3) 2 (1, 4) 3 (1, 4) 4 (2, 5, 6) 5 (4, 6) 6 (4, 5)
    3. 1 (2, 3) 2 (1, 4) 3 (1, 4) 4 (2, 3, 5, 6) 5 (4, 6) 6 (4, 5)
    4. 1 (2, 3) 2 (1, 4) 3 (1, 4) 4 (1, 3, 5, 6) 5 (4, 6) 6 (4, 5)
    
    
36. Taking the graph from the previous question,
    which of the following would be an adjacency matrix representation of this graph?

    1. 0	1	1	0	0	0
       1	0	0	1	0	0
       1	0	0	1	0	0
       0	1	1	0	1	1
       0	0	0	1	0	1
       0	0	0	1	1	0

    2. 0	1	0	0	0	0
       1	0	0	1	0	0
       1	0	0	1	0	0
       0	1	1	1	1	1
       0	0	0	1	0	1
       0	0	0	1	1	0

    3. 0	1	1	0	0	0
       1	0	0	1	0	0
       1	0	0	1	0	1
       0	1	1	0	1	1
       0	0	1	1	0	1
       0	0	0	1	1	0

    4. 0	1	1	0	0	0
       1	0	0	1	0	0
       0	0	0	1	0	0
       0	1	1	0	1	1
       0	0	0	1	0	1
       1	0	0	1	1	0

    
    
37. Besides running time, we can also measure algorithm performance by:
    1. amount of disk-memory communication
    2. number of processors used
    3. amount of network bandwith used
    4. all of the above *
    
    
38. An advantage of the adjacency matrix representation over the adjacency list representation is
    1. it is smaller.
    2. it allows quicker searches for determining whether some edge exists. *
    3. it can represent weighted graphs.
    4. it can represent directed graphs.
    
    
39. Which of the following matrices represents this directed graph:
    
    

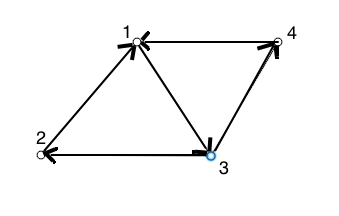
    1. 0	0	1	0
       0	1	1	0
       0	1	1	0
       0	0	1	0

    2. 0	1	1	0
       0	1	1	0
       0	1	1	0
       0	1	1	0

    3. 0	0	1	0
       1	0	0	0
       0	1	1	0
       1	0	0	1

    4. 0	0	1	0
       1	0	0	0
       0	1	0	1
       1	0	0	0

    
    
40. A breadth-first search of this graph:
    
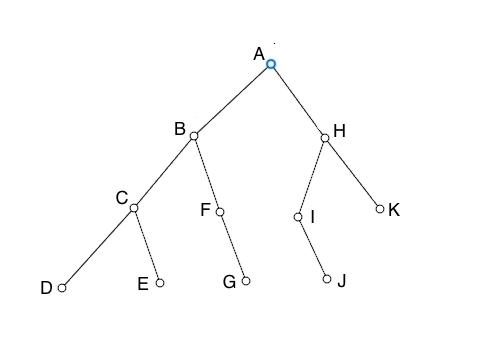
    Will cover the nodes in what order?
    1. A-B-C-D-E-F-G-H-I-J-K
    2. A-C-B-H-E-F-I-K-G-J-D
    3. A-B-H-C-F-I-K-D-E-G-J *
    4. A-B-C-H-F-I-K-D-E-G-J
    
    
41. Θ-notation applied to a function implies it is
    1. a function we know little about.
    2. asymptotically bound from above and below. *
    3. asymptotically bound from below only.
    4. asymptotically bound from above only.
    
    
42. Using the master theorem, the solution to the recurrence
    T(n) = 3T(n/3) + n/2 is:
    1. Θ(n/3)
    2. Θ(n log n) *
    3. Θ(n)
    4. the master theorem can't be applied here.
    
    
43. Dynamic programming is preferred to simple recursive solutions when
    1. the recursive solution is hard to grasp.
    2. all of the sub-problems are completely independent of each other.
    3. the recursion goes beyond 4 levels.
    4. the same sub-problems must be solved multiple times. *
    
    
44. Direct dictionaries are only practical when
    1. the number of keys is small. *
    2. we don't care how slow lookups will be.
    3. we aren't worried about the large number of collisions hashing will produce.
    4. linear probing is appropriate.
    
    
45. A greedy algorithm is appropriate when
    1. we need to consider the global situation when making any choice.
    2. there is extensive over-lap among sub-problems.
    3. only the locally best choice matters. *
    4. greed is the goal of the algorithm choice.
    
    
46. We can use a greedy algorithm to solve
    1. a rod-cutting problem.
    2. a minimum-spanning-tree problem.
    3. a matrix-parenthisization problem.
    4. a shortest-path problem.
    
    
47. If f(n) = ω(g(n)), that means
    1. g dominates f asymptotically
    2. f is bounded below by g asymptotically
    3. f is bounded above by g asymptotically
    4. f dominates g asymptotically *
    
    
48. Using the master theorem, the solution to the recurrence
    T(n) = 64T(n/8) - n² log n is:
    1. Θ(n²)
    2. Θ(n⁴ log n)
    3. Θ(n² log n)
    4. the master theorem can't be applied here.
    
    
49. The worst-case running time of a search on a binary search tree is
    1. θ(n²)
    2. θ(n) *
    3. θ(lg n)
    4. θ(1)
    
    
50. A toppological sort on a tree makes use of
    1. breadth-first search.
    2. finding the minimum spanning tree.
    3. depth-first search.
    4. finding the shortest path.
    
    

Problems

1. Let us say we have an algorithm that runs in 10n² + 10 time. We want to show its order of complexity is θ(n²). Give an example of a set of k₁, k₂, and n₀ that would do this.
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
2. How will a depth-first search process the following tree?
   Write a number above each vertex indicating the order in which it will be visited:
   
   
3. Use an indicator random variable to show how many numbers we have to pick from a set of n numbers before we are more likely than not to have drawn the same number twice.
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
4. Describe why the fractional knapsack problem can be solved with a greedy algorithm, but the whole unit problem cannot.
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
5. Prove that Kruskal's algorithm can correctly find a minimum spanning tree.