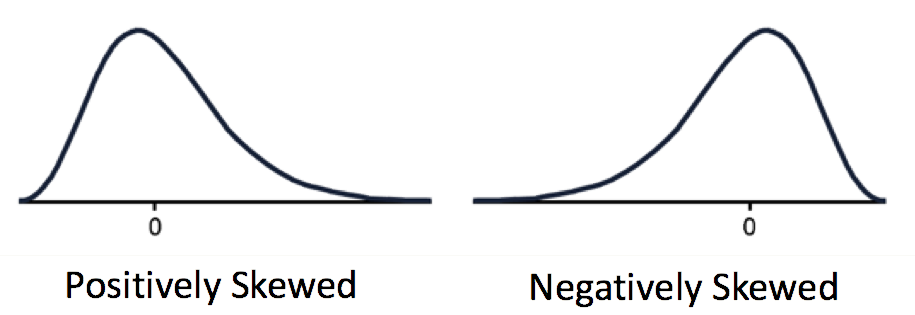
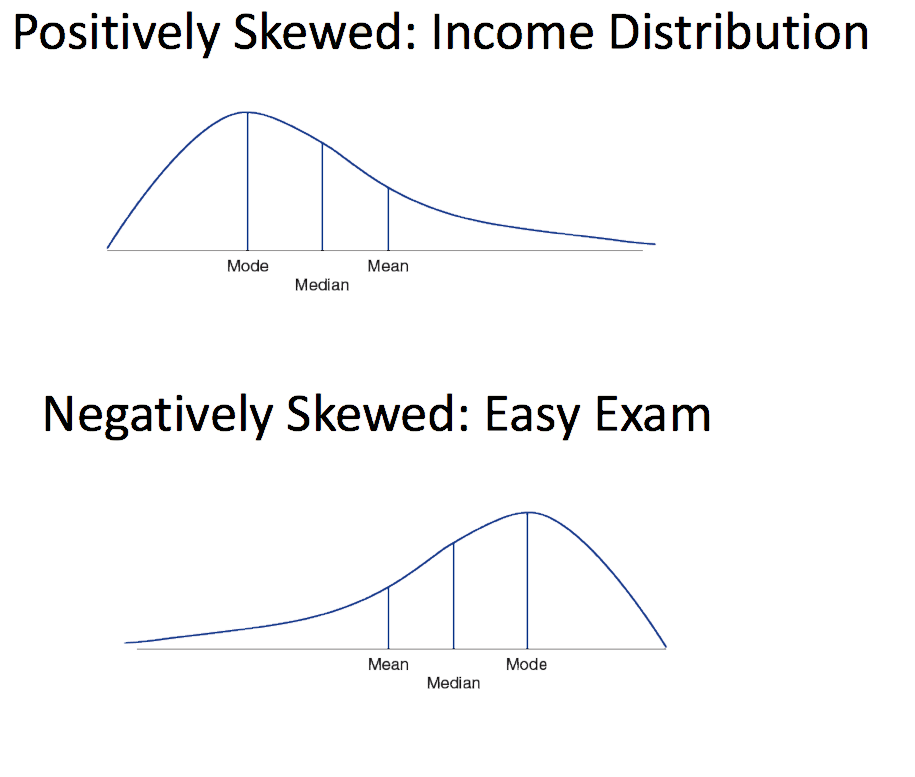
Describing Interval and Ratio Data

Introduction

Now let us look at the effects of skewness on our three averages (measures of central tendency).

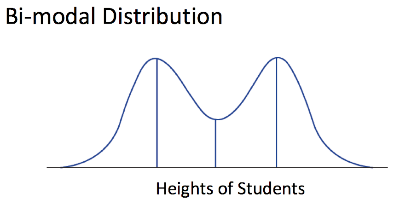
Many distributions show a bimodal pattern:

Measurement of the Variability of Interval and Ration Data

Khan Academy course on spread

When the Data Are Skewed

Central tendency: use the median not the mean.
Variability: use the range not the standard deviation.

When the Data Are Normally Distributed

"How deep is this river?"
"Oh, on average only about two feet."

Population and Sample: Statisticians' Way of Saying 'All' and 'Some'

Sampling
Range
The spread of values.
Example: the range of grades was 63 - 98, or 35.
Variance

The average of the squared distance of all data points from the mean.
For each data point:
- Calculate its distance from the mean.
- Square that.
- Sum those squared figures.
- Divide that sum by n, the number of data points.
- Take the square root of the variance.
Why square the distance?
Consider two data samples, eaach with a mean of 5:
Sample 1: 2, 3, 4, 5, 6, 7, 8
Sample 2: 0, 5, 10
The sum of distances for Sample 1 is 12.
(3 + 2 + 1 + 0 + 1 + 2 + 3)
The sum of distances for Sample 2 is 10.
(5 + 0 + 5)
Looks like Sample 1 has more variability!
Instead sum the squares of the distances:
Sample 1: 9 + 4 + 1 + 0 + 1 + 4 + 9 = 28
Standard Deviation
The square root of the variance.

Khan Academy on measures of spread

Reporting the Calculated Value of the Mean and Standard Deviation

μ = 75.8, SD = 4.31

Effects of arithmetic operations

Adding or subtracting a constant moves the whole distribution. The mean moves, the spread remains unchanged.
Multiplying or dividing by a constant spreads or narrows the distribution. The standard deviation is multiplied (or divided) by that constant.

What You Always Wanted to Know About IQ

We can divide a distribution into different segments:

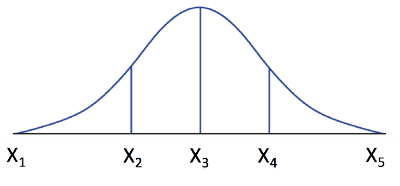
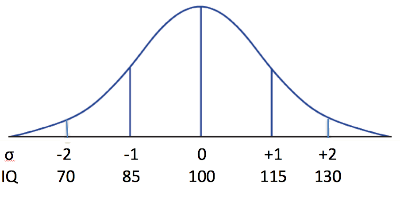
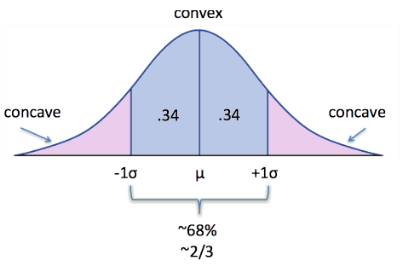
The standard deviation, in particular, divides the normal distribution as follows:

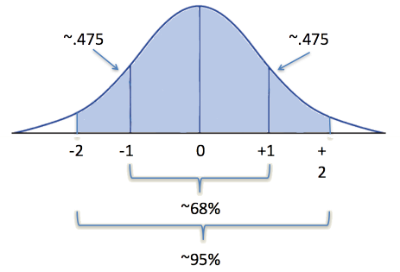
Standard deviation and the normal distribution

And now let's look two standard deviations out:

95% of population is within two σ of the μ.

The IQ test was designed around a normal distribution. The mean is kept at 100, and the scores are calibrated so that 15 points = 1 SD.

Descriptive Statistics: The z Score

Descriptive Statistics	Nominal	Ordinal	Interval / Ratio
Frequency distr.	Bar or pie chart	Bar chart	Histogram
Central tendency	Mode	Median	Mean
Variability	NA	Range	Standard devation and z value

A Little History and a Very Impressive Equation

There is a very complicated equation that describes the normal distribution.
We aren't going to worry about it.
However, we should know that the normal distribution:

Is unimodal
Is symmetrical
Is bell-shaped
Can be transformed into a standard normal curve.
Has inflection points 1 SD above and below the mean.
We use z scores in dealing with it.

The Standard, Very Important, z Score

z score: the number of standard deviation a score is from the population mean.

Computing Apples and Oranges?

The z Table