Finding Differences with Nominal Data I: Goodness-of-Fit Chi-Square

Introduction

Some concepts from Chapter 6 we need.

Independent variable
Manipulated by the experimenter
Dependent variable
Not manipulated by the experimenter
Null hypothesis
Nothing is going on!
Alternative hypothesis
Something's happening here!
alpha
If the null hypothesis is true, how likely is our result?
Type I error
We reject the null hypothesis, although it is true.
Type II error
We accept the null hypothesis, although it is false.
Crucial point: if we decrease the chance of a type I error, we increase the chance of type II, and vice versa.

Another thing to discuss: what is the height of the average animal?
Number of insects is estimated to be roughly 1,000,000,000,000,000,000. By comparison, the number of humans is 7,000,000,000.
What is the mean weight of all animals going to be?
What is the mean weight of all humans?
Do we expect to see a human 1000 times the mean weight? Do we expect to see an animal 1000 times the mean weight?

Another topic: error in scientific measurement and the normal distribution.
The story of the English mint.

First Example

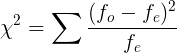
f_o: observed frequency
f_e: expected frequency

The professor gets you to gamble with him, betting on tosses of his "fair" coin. He takes heads, and the first ten tosses come up heads seven times.
Should you accuse him of cheating?

The χ² test typically uses the α = .05 cutoff for determining the critical region or the area of rejection.
If the χ² value is greater than the value in our table, we reject the null hypothesis.

Another Example

The professor gets you to gamble with him, betting on tosses of his "fair" coin. He takes heads, and the first ten tosses come up heads nine times.
Should you accuse him of cheating?

Very important: significant means something very specific in statistics: it just means the result is in the (arbitrarily chosen) critical region.

A Final Example

Important concept: degrees of freedom (df).
A toss of a die has 5 degrees of freedom: once you know the die was not 1 - 5, you know it was 6.
With more degrees of freedom, we expect more difference from the expected value.

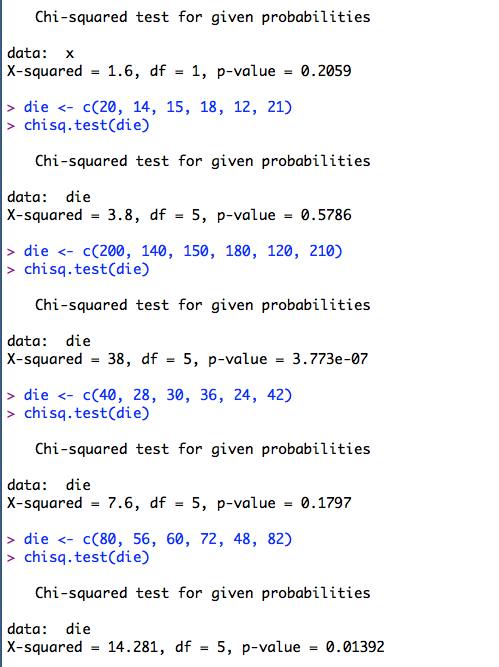
H₀: we have fair dice.
H₁: we don't have fair dice.

We toss the die 100 times, and get 20 ones, 14 twos, 15 threes, 18 fours, 12 fives, and 21 sixes.

Running the test on multiples of the original dice numbers

Purpose and Limitations of the Chi-Square Test

The test compares observed and expected frequencies. This means we must already know an expected frequency!
The test just says whether something unexpected occurred. We must examine the data to see what that was, e.g., too many sixes in our dice rolling.
The test does not incorporate any measure of effect size, a topic taken up later in our textbook.
Expected frequencies must be at least five for the test to apply. (We can see why if we contemplate tossing a coin a single time and trying to apply a χ² test to the result!)

Assumptions of the Chi-Square Test

The data are in the form of frequencies.
The observations are independent.

Extras