
Informally, a set is a collection of objects. Often, these are
mathematical objects, but they need not be. The
populations
studied in statistics can be regarded as sets.
No object can be included in a set multiple times.
Examples:
We can define a set by listing its members. The
notation is:
A = {1, 2, 3, 4, 5, 6}
This might be the set of possible rolls of a six-sided
die.
Or we can use a rule based definition. If we want all
even integers, we could write:
A = {x: x is even}

Let us define A as "the set of all states in the U.S."
Then we might define two more sets as R = "the set of
states that voted for Romney in 2012," and O = "the set
of all states that voted for Obama in 2012."

Then R and O are both subsets of A. We define
a subset of a set A as any set that contains only
members A.
Our notation here is:
R ⊆ A
O ⊆ A
Note that under this definition, A is a subset of
itself. We also can define proper subsets of A:
these contain only members of A but not all members
of A. Both R and O are also proper subsets of A. Our
notation is:
R ⊂ A
O ⊂ A
We say two sets are equal if they contain the same members. So, if A = {1, 2, 3} and B = {3, 2, 1}, then we can write A = B. (Order does not matter!)
The union operator combines two sets so that the new
set contains all of the elements of each of the two.

If today's baseball game is the Angels versus the
Yankees, then the "set of all players" (P) is the union of
the "set of all Angels players" (A) and the "set of all
Yankees players" (Y).
Our notation here is:
P = A ∪ Y
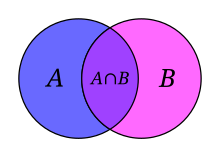
The intersection of two sets contains only the elements
that are in both sets. So if R = {the states
that have voted for a Republican candidate for
president since 2000} and D = {the states
that have voted for a Democratic candidate for
president since 2000} then their intersection is the
states that are not pure red or pure blue in this map:

This would be the set of swing states, S.
Our notation here is:
S = R ∩ D
We can define the universe of some group of sets
as the collection of all possible members. So if we were
surveying American voters, then U = {all American voters}.
Or if we are considering American states, then U = {all
American states}.
Then, if O = Obama states, and R = Romney states, those
sets are complements. We have:
O ∪ R = U
O ∩ R = ∅

These diagrams are a great way to get a picture of the ideas of
set theory. We depict a set as a circle.
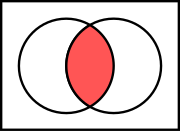
Then, for the intersection of two sets, we have the diagram:
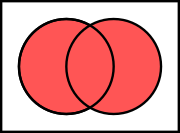
Or for the union of two sets, we have the diagram:
Finally, if A is the set in the left circle below, the
complement of A is:
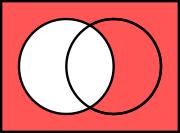

In English: the bar over the symbols means essentially "not."
And what is comprised by each equation is the area in
blue.
So:
Law 1: what is not in the union of
two sets is the intersection of
what is not in one of them and what is not in the other of
them.
Example:
U (our universe) = "people authorized to be on our campus"
"The people authorized to be on our campus
who are not either students
at St. Joseph's College or faculty at St. Joseph's
College" (a union of two sets) is equivalent to "The people
authorized to be on our campus who are not on the list of
students and who are not on the list of faculty" (an
intersection of two sets). This set would include
administrators, workers at the cafeteria, visitors with passes,
security personnel, and so on.
Law 2: what is not in the intersection of two sets is
the union of what is not in one of them and
what is not in the other of them.
Example:
U (our universe) = "people authorized to be on our campus"
"The people authorized to be on our campus
who are not both students
at St. Joseph's College and faculty at St. Joseph's
College" (an intersection of two sets) is equivalent to "The people
authorized to be on our campus who
are not students or who are
not faculty" (a union of two sets). This set contains everyone
authorized on campus who is not a
student and a faculty member.
(Last semester, that set might have excluded only me!)