- Reduce Type I error to 0
- Reduce Type II error to 0
- Eliminate some Type I error, but only by increasing Type II error
- All of the above
What percentage of measurements were less than 10 calories?
- 50%
- 10%
- 20%
- 100%
- 50%
- 10%
- 20%
- 100%
- 16%
- 95%
- 34%
- 68%
- 2%
- 8%
- 16%
- 47%
- Less than 10%
- Over 50%
- Less than 0%
- Less than 1%
- Less than 1%
- About 95%
- About 5%
- About 50%
- Very suspicious: it is massively unlikely.
- Nothing to see here; move along!
- It definitely confirms the scientists was faking their results.
- Not enough information.
- a personal belief
- a real number between 0 and 1
- an integer greater than one
- a question Tornike will never get right
Here is your actual outcome when Kenneth deals you the cards:
| Suit | fo | fe |
|---|---|---|
| Hearts | 11 | 6 |
| Diamonds | 2 | 6 |
| Spades | 3 | 6 |
| Clubs | 8 | 6 |
In this situation, the null hypothesis should be:
- The deal is fair
- Kenneth looks like a card shark, so the deal is most likely unfair
- Why is the professor picking on Kenneth?
- Can't say
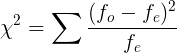
- 90
- 18
- 9
- 1
- reject the null hypothesis
- fail to reject the null hypothesis
- conclude with certainty that Kenneth was cheating
- not enough information
- reject the null hypothesis
- fail to reject the null hypothesis
- conclude with certainty that Kenneth was cheating
- not enough information
- why are there only four categories?
- all of those sixes look fishy
- too many clubs
- too many hearts; too few diamonds
| Suit | fo | fe |
|---|---|---|
| Hearts | 6 | 6 |
| Diamonds | 5 | 6 |
| Spades | 4 | 6 |
| Clubs | 9 | 6 |
We get a Χ2 of:
- 3.8
- 2.3
- .7
- 12.8
- reject the null hypothesis
- fail to reject the null hypothesis
- conclude with certainty that Davia was cheating
- not enough information
- reject the null hypothesis
- fail to reject the null hypothesis
- conclude with certainty that Davia was cheating
- not enough information
- nominal data
- ordinal data
- ratio data
- interval data
- 7
- the number of categories
- the number of categories plus one
- the number of categories minus one
- reject the null hypothesis
- accept the null hypothesis
- do the experiment over; something went wrong
- conclude that Kenneth is cheating