

Tree
A tree is a connected graph with no circuits and a unique simple path between any of it's vertices.
Forest
Forest is a graph containing zero or more disjoint trees.
Definition:
A rooted tree is an acyclic graph, with one vertex designated as root.

A tree with n vertices has n − 1 edges.
A full m-ary tree with i internal vertices contains n = m*i + 1 vertices.
A full m-ary tree with
There are at most mh leaves in an m-ary tree of height h.
Trees provide easier location of items. Depending on a certain property, items are stored in a tree data structure for faster retrieval.
Prefix codes are coding schemes in which no codeword
is a prefix of a different codeword.
This makes decoding easier -- no lookahead.
(else and else-if)
It means that we never hit two letters on the same path
down the tree!
| a | b | c | d | e | f | |
|---|---|---|---|---|---|---|
| Frequency (in 1000s) | 45 | 13 | 12 | 16 | 9 | 5 |
| Codeword | 0 | 101 | 100 | 111 | 1101 | 1100 |

Huffman coding is away of compressing data
that consists of characters buy creating
short binary representations for the
characters that occur most frequently
in the data, and using longer representations
for characters that occur less frequently.
We build a binary tree from the bottom-up,
starting with the two least-frequent characters,
and building up from there. This ensures the
least-frequent characters have the longest codes.
Consider the phrase "Mississippi River".
This is 136 bits in 8-bit ASCII encoding.
Here is the Huffman coding for it:
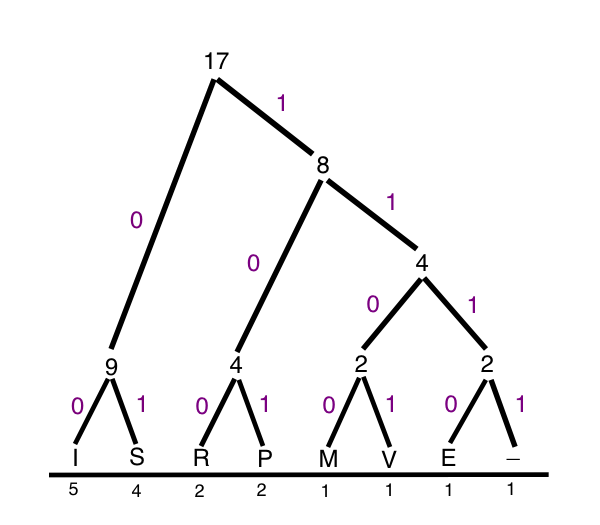
I = 00
S = 01
P = 100
R - 101
M = 1100
V = 1101
E = 1110
_ = 1111
The final string:
110000010100010100100100001111101001101101
Try parsing it, and convince yourself that
there is only one possible interpretation
of it. That is what the prefix coding buys us.
Trees can be used to analyze certain type of games like tic-tac-toe where there is no element of chance and previous move is known to each player.
The vertices of trees represent position that a game can be in as the game progresses, the edge represent legal moves between these positions
Game trees can be simplified by representing all symmetric positions of game by the same vertex.
However, same position of the game may be represent by different vertices if different sequences of moves lead to this position.

Preorder pseudocode:
preorder(T):
if T == nil:
return
else:
print(T)
preorder(T.left)
preorder(T.right)

Inorder pseudocode:
inorder(T):
if T == nil:
return
else:
inorder(T.left)
print(T)
inorder(T.right)

Postorder pseudocode:
postorder(T):
if T == nil:
return
else:
postorder(T.left)
postorder(T.right)
print(T)
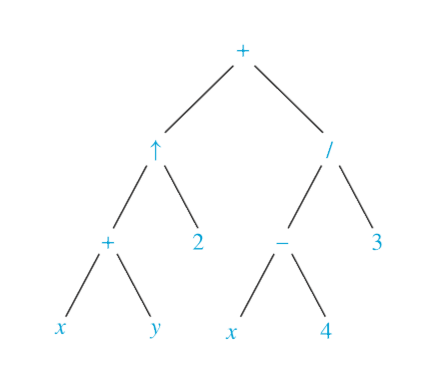
Prefix form: + ^ + x y 2 / - x 4 3
Postfix form: x y + 2 ^ x 4 - 3 / +
The spanning tree of a graph G is a subgraph of G that is a tree and that contains every vertex of G.
A graph is connected if and only if it has a spanning
tree.
We prove this by removing edges from circuits.

This is a way to find a spanning tree in a connected
graph (or detect that the graph is unconnected).
The edges used to form that tree are called
tree edges.
The edges not used in forming that tree are called
back edges (because they lead back
to a node already visited). If there are back edges,
they show that circuits exist in the graph. And if
there are unvisited vertices when DFS is done,
then the graph is not connected.
So, DFS can:
An electrical grid in an area can be thought of as a weighted graph.
There is a certain cost attached to forming a grid which depends on the area, the distance between two poles and certain other factors.
We can think of all the poles to be vertices and the cost of forming a connection as the weighing factor.
We can form a Minimum Spanning Tree to determine the minimum cost of total connection.
Minimum Spanning Trees from DAA