Design and Analysis of Algorithms: Greedy Algorithms


A family of problems and approriate solutions

It is important to recognize that we have been dealing with a family of problems and solutions to those problems:

What is a greedy algorithm?

We have an optimization problem.
At each step of the algorithm, we have to make a choice, e.g., cut the rod here, or cut it there.
Sometimes, we need to calculate the result of all possible choices.

But sometimes, we can do much better than either of those choices. Sometimes, we don't need to consider the global situation at all: we can simply make the best choice among the options provided by the local problem we face, and then continue that procedure for all subsequent local problems.

An algorithm that operates in such a fashion is a greedy algorithm. (The name comes from the idea that the algorithm greedily grabs the best choice available to it right away.)

Clearly, not all problems can be solved by greedy algorithms. Consider this simple shortest path problem:



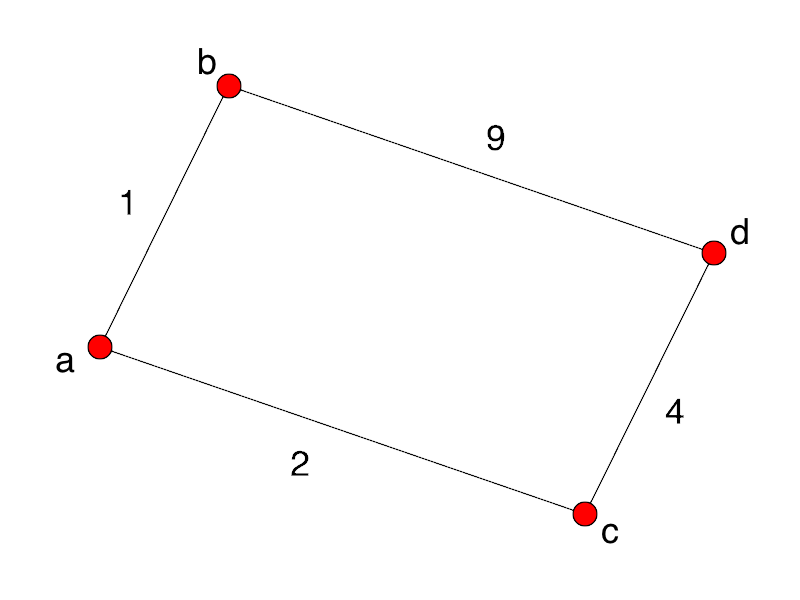
A greedy algorithm choosing the shortest path from a to d will wrongly head to b first, rather than to c.

Introduction to greedy algorithms
An activity selection problem

Suppose we need to schedule a lecture hall with the goal of maximizing the number of lectures it can hold, given the constraint that no lectures can share the space.
We have the activities sorted in order of increasing finish time:
f1 ≤ f2 ≤ f3 ≤ ... ≤ fn - 1 ≤ fn.

We might have the following set of activities:

i 1 2 3 4 5 6 7 8 9 10 11
si 1 3 0 5 3 5 6 8 8 2 12
fi 4 5 6 7 9 9 10 11 12 14 16


We have several sets of mutually compatible lectures, e.g.:
{a3, a9, a11}
However, this set is larger:
{a1, a4, a8, a11}

How do we find the maximum subset of lectures we can schedule?

The optimal sub-structure of the problem

It is easy to see that the problem exhibits optimal substructure. If the optimal solution includes a lecture from 4 to 6, then we have the sub-problems of scheduling lectures that end by 4, and lectures that start at 6 or after. Obviously, we must solve each of those sub-problems in an optimal way, or our solution will not be optimal! (Think of our problem of traveling from MetroTech Center to Yankee Stadium via Grand Central.) Our textbook calls this a "cut-and-paste" argument: we can cut an optimal set of lectures ending by 4 and paste it into our supposed optimal solution: if the solution was different before 4, we have improved it, so it wasn't actually optimal!

It is straight forward to see that we can solve this problem with a recursive, memoized algorithm -- we examine each possible "cut" of a "middle" lecture, and recursively solve the start-to-middle problem, and the middle-to-end problem. Or we could use a bottom-up dynamic programming algorithm, developed from the recursive solution in the same way we saw in our last lecture.

Making the greedy choice

But we can solve this problem much more efficiently. At each step in solving it, we can make a completely local choice: what activity (still possible) finishes earliest?

Since we have sorted the activities in order of increasing finish time, we simply choose a1, since it is guaranteed to finish at least tied for first.

The proof that this will give us a maximal set of activities is trivial: Let us suppose aj is the activity in some set that finishes first, but that there is a maximal subset Ak that does not include aj. We simply remove the first element of Ak and substitute in aj. This is guaranteed to be a compatible set of activities, since aj finishes first, and it will be maximal, since it is the same size as Ak. (Note that the textbook offers us an example of such sets on page 415.)

A recursive greedy algorithm

The algorithm is straightforward: find the first compatible activity, then call the algorithm again with the rest of the activity list.

One trick worth noting: the authors put a dummy activity in the first position of the list, so that there is no special first call of the function.
There is a design pattern here: oftentimes, it is better to modify a data structure than to do special coding for end cases. 

            Recursive-Activity-Selector(s, f, k, n)
                m = k + 1
                while m ≤ n and s[m] < f[k]
                    m = m + 1
                if m ≤ n
                    // + here is set union!
                    return a[m] + Recursive-Activity-Selector(s, f, m, n)
                else
                    return NIL

An iterative greedy algorithm

As usual, it is fairly simple to transform the recursive algorithm into an iterative version. The authors discuss tail recursion in this section: let's review what this is. 

            Greedy-Activity-Selector(s, f)
                n = s.length
                A = {a[1]}
                k = 1
                for m = 2 to n
                    if s[m] > f[k]
                        A = A + {a[m]} // + is set union!
                        k = m
                return A

Run the python code for greedy activity selector

In the console below, type or paste:
!git clone https://gist.github.com/bb22ea72d8b15fa965d2f50e6798ae50.git
cd bb22ea72d8b15fa965d2f50e6798ae50
from greedy_algorithms import *
print("start: ", start, "\nfinish: ", finish)
greedy_activity_selector(start, finish)

Python console
Elements of the greedy strategy

  1. Determine the optimal substructure of the problem.
  2. Develop a recursive solution.
  3. Show if we make the greedy choice, that only one sub-problem remains.
  4. Prove that it is always safe to make the greedy choice.
  5. Develop a recursive algorithm that implements the greedy strategy.
  6. Convert the recursive algorithm to an iterative algorithm
Greedy-choice property



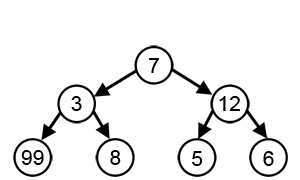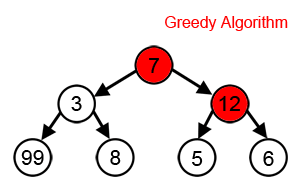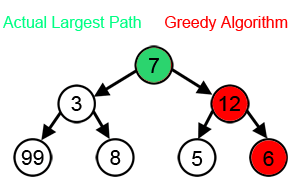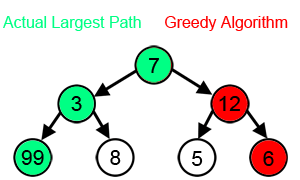
For a greedy algorithm to work, the optimal choice must not depend upon any sub-problems or any future choices.

To prove that a greedy choice will be appropriate for some problem, we typically examine an optimal solution, and then show that substituting in a greedy choice will also yield an optimal solution.

Optimal substructure

This is simpler then for dynamic programming problems: all we need to do is show that a greedy choice combined with an optimal solution to the sub problem of the rest of the data gives us an optimal solution to the original problem. We use induction to show that making the greedy choice at every step produces an optimal solution.

Greedy versus dynamic programming

Two knapsack problems:

  1. A thief can take entire items from a store or not, and put them in his knapsack.
  2. A thief can take whatever fraction of an item he wants, and put it in his knapsack.

The latter can be solved with a greedy algorithm, the former cannot.

Huffman codes



Hoffman coding is away of compressing data that consists of characters buy creating short binary representations for the characters that occur most frequently in the data, and using longer representations for characters that occur less frequently.

Huffman coding
Prefix codes

Prefix codes are coding schemes in which no codeword is a prefix of a different codeword.
This makes decoding easier -- no lookahead. (else and else-if)
It means that we never hit two letters on the same path down the tree!

a b c d e f
Frequency (in 1000s) 45 13 12 16 9 5
Codeword 0 101 100 111 1101 1100
Constructing a Huffman code

We build a binary tree from the bottom-up, starting with the two least-frequent characters, and building up from there. This ensures the least-frequent characters have the longest codes.

Consider the phrase "Mississippi River". This is 136 bits in 8-bit ASCII encoding.

Here is the Huffman coding for it:


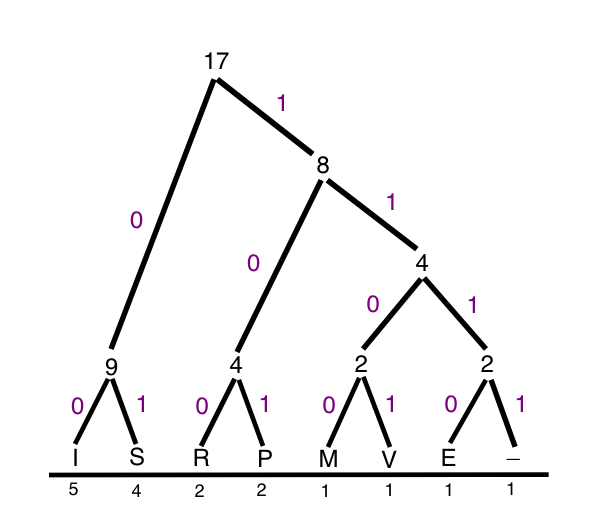
I = 00
S = 01
P = 100
R - 101
M = 1100
V = 1101
E = 1110
_ = 1111

The final string:
110000010100010100100100001111101001101101

Try parsing it, and convince yourself that there is only one possible interpretation of it. That is what the prefix coding buys us.

Correctness of Huffman's algorithm

We begin operating on an alphabet Σ. At each step, we create a new alphabet, Σ', with two symbols of Σ replaced by a new "meta-symbol".

Base case: For an alphabet of two symbols, the algorithm outputs 0 for one of them, and 1 for the other. And that is clearly optimal! (An alphabet of size 1 is a non-problem!)

Inductive step: Assume the algorithm is correct for input of size n - 1.
At each step in the algorithm, we replace the two least frequent remaining symbols a and b with a new symbol ab, whose probability is the sum of the probabilities of a and b.
We always want the lowest frequency symbols to have the longest encoding length.
Any choice among symbols at the lowest frequency will be fine, since they all have equally low frequency. So we can pair any of those lowest frequency symbols as we wish.
Now assume that there is an encoding Σ'' that is derived from Σ (like Σ') but differs in choosing to combine x and y into a xy. But since we made the greedy choice, xy can be at best tied with ab meaning Σ'' is at best another optimal encoding, and our encoding Σ' is optimal after all.

Matroids and greedy methods

Matroids

A graph

Consider the following graph, where the edges represent roads and the vertices towns:



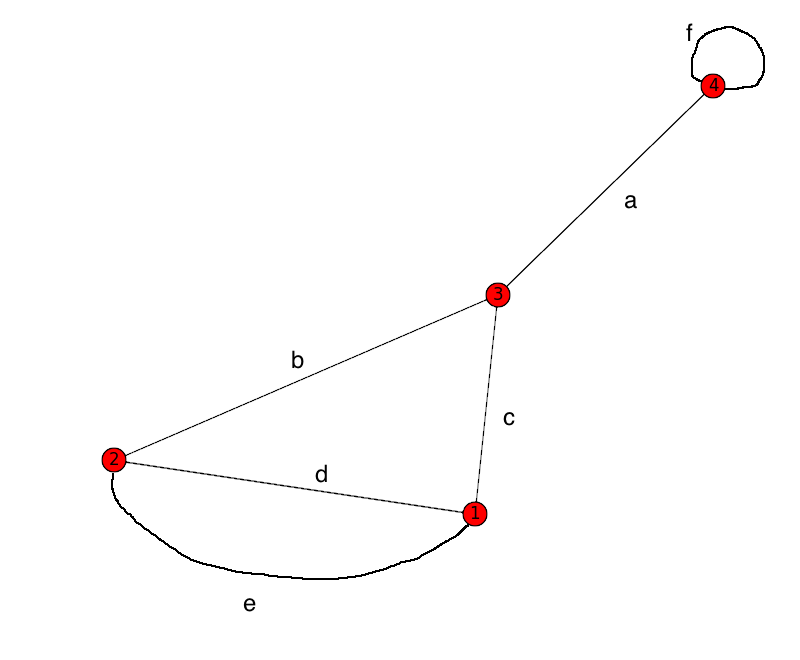
If we want to build a set of roads that are only built if there is no other route between towns, what sets are possible?

Notice:

A vector space

Now look at the following vector space in ℝ3:


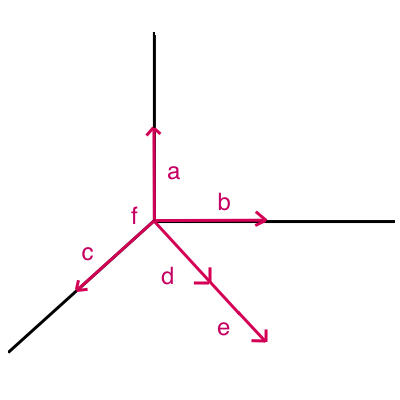
(f is the vector 0, 0, 0.)

What sets of linearly independent vectors are possible?

Notice:

A matching problem

You live in a small town with 3 women and 5 men who are single but might be married off. There is a town matchmaker who makes money by arranging marriages, and so he wants to arrange as many as possible.
In this town, it's "ladies' choice," and the women are numbered 1-3, and the men are a-f.



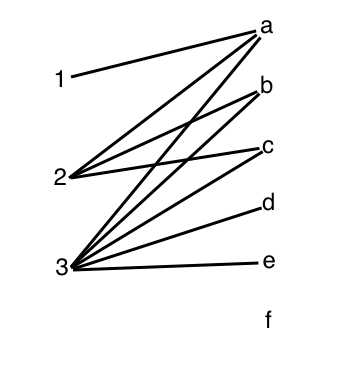
What sets of matches are possible?

Notice:

The definition of a matroid

We are looking at general conditions for independence of choices. All three situations turn out to be surprisingly similar. They can all be modeled using matroids.

We have a matroid when the following independence conditions are satisfied:

  1. ∅ is independent.
  2. If set J is independent and I is a subset of J, then I is independent.
  3. If I and J are independent, and cardinality(I) < cardinality(J), then there is some j in J and not in I, so that I ∪ j is also independent.

A matroid consists of (S, I), where S is a set, and I is a set of subsets of S, for which axioms 1-3 above are satisfied.

All three situations described above, the vector space, the graph, and the matching problem, turn out to be the same matroid. (Technically, they are isomorphic matroids.)

The bases of a matroid

A subset in I is a basis for a matroid if it is a maximal subset, which here means it is not contained in any larger subset that is in I.

So in the above examples, the bases are:
{a, b, c} {a, b, d}, {a, b, e} {a, c, d} {a, c, e}

Theorem: Every basis of a matroid is of the same size.
Proof: Let assume that there are some bases A and B of a matroid such that |B| < |A|.
Then by the exchange axiom (#3 above), there is some element a of A that can be moved into B, and B will still be independent.
Therefore, it was not a maximal independent subset after all!

Translation into the different matroid realms:

The dimension of a vector space is the size of any of its bases.

Every spanning tree has the same number of edges.

We are proving things about vector spaces and graphs simply by examining the axioms of matroids!

Credit

This section draws on lectures by Federico Ardila: here and here.

Greedy algorithms on a weighted matroid

Q: Why do greedy algorithms work on a matroid?
A: Independence!

We often have a problem that can be considered as an instance of finding a maximum (or minimum) weight independent subset in a weighted matroid. Let us look at Kruskal's algorithm.

A task-scheduling problem as a matroid



The surprise here is that we can simply greedily grab tasks in order of increasing deadlines, and our algorithm will work.

Source Code

Java
Ruby
Go
Python

For Further Study
Homework
  1. Our intuition might tell us that choosing the shortest subway path from MetroTech Center to Yankee Stadium is a simpler problem than choosing a minimum spanning tree for all New York subway stations. Yet the latter can be solved with a greedy algorithm, while the first cannot. Why?

    Answer: The spanning tree problem is a matroid, and so deals with indpendent sub-problems. The different paths between subway stops are not independent: some choices foreclose other choices.
  2. Why is the run-time analysis of the rod cutting problem not the same as that of the matrix chain problem?

    Answer:The matrix chain order problem can nest the sub-problems in many ways, while the rod-cutting problem simply makes one level of cuts. It would be more like the matrix problem if it also bundled packages of cut rods into higher level bundles.
    Or, rod cutting: ---|--|--|--|------|--
    The vertical lines represent cuts.
    Whereas, matrix chaining: (((A A) (A (A A))) (A A) ((A A A)) A)
  3. For the activity selection problem, besides simply choosing the activity this finishes first, what other greedy choices could we make?

    Answer: The activity that starts first, the activity with the smallest time requirement.
  4. On page 419, line 2 of pseudo-code loops, and the comment describing why it is looping is incorrect. What is actually going on there? Why isn't the code just grabbing the first element in the activity array, which must be the one that finishes first?

    Answer: The code has to find not the first activity that finishes, but the first one that starts after the "current" time and finishes first. So it must loop until it finds that item.
  5. Show that the fractional knapsack problem (p. 425) has the greedy choice property.

    Answer: We can take as much as possible of the highest value per weight item first. If we fill the knapsack, we are done. If not, we can take as much as possible of the second-highest value item, and repeat until the knapsack is full. Each choice is completely independent of subsequent choices.